Cheat Sheet

Chomsky-Hierarchien

Typ der Sprache	Sprache / Grammatik	Akzeptiert von
Typ-0	Rekursiv aufzählbare	Turing-Maschine (TMs)
Typ-1	Kontextsensitive	Linear Bandbeschränkte Automaten (LBAs)
Typ-2	Kontextfreie	Kellerautomaten (KA) / Push-Down Automaton (PDA)
Typ-3	Reguläre	Endlichen Automaten

Umwandlung NEA in DEA (Potenzmengenkonstruktion)

Umwandlung kann mit tabellarischer Darstellung gemacht werden:

Von ($D_n$ = $N_n$ / $\text{Eingabe}$)	NEA	DEA
Start	(Startzustand)	(Startzustand)
…	…	…

“Quantenzustände”, also Übergange in einem DEA bei denen ein NEA sich in zwei verschiedenen Zuständen befinden könnte, werden durch das Zusammenfassen der beiden Zustände in einem weiteren Zustand des DEA abgebildet ($D_{ex}=\{N_{ex1},N_{ex2}\}$)

Die Tabelle wird gelesen als: “Ich befinde mich in Zustand $D_n$, welcher equivalent zu $N_n$ ist und mache eine $Eingabe$. Dadurch lande ich beim NEA in … und beim DEA in …”

Regulärer Ausdruck aus NEA (Zustandselimination)

Mit der Zustandselimination kann aus einem NEA ein regulärer Ausdruck erzeugt werden. Die Zustandselimination verwendet sog. verallgemeinerte NEAs (VNEAs), um den regulären Ausdrück möglichst einfach zu erreichen (links ist ein NEA, rechts ein VNEA):

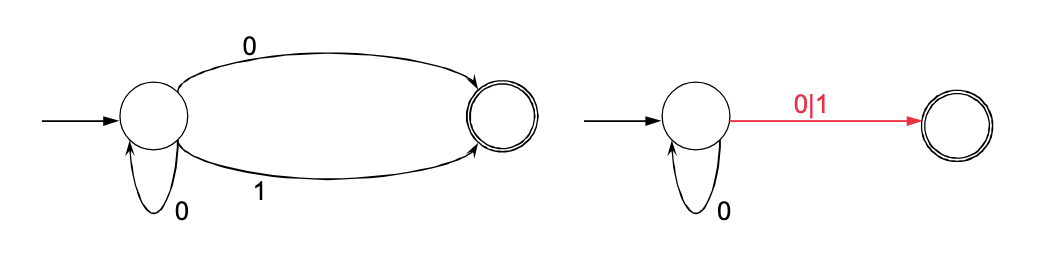
Bei der Zustandselimination wird folgendes gemacht:

1. Wandle den NEA in einen VNEA um
2. Wiederhole für alle Endzustände $q\in F$:
   1. Eliminiere (iterativ, also nacheinander, nicht gleichzeitig!) alle Zustände außer dem Startzustand $q_0$ und $q$.
   2. Bilde einen regulären Ausdruck aus dem finalen Automaten
3. Vereinige die Ausdrücke für alle Endzustände q mit einem logischen Oder (|)
   1. Bilde die Summe aller entstandenen regulären Ausdrücke

Reguläre Ausdrücke, EAs und Syntaxdiagramme

Zu jedem regulären Ausdruck gibt es einen endlichen Automaten, den man aus dem regulären Ausdruck hinaus erschließen kann.

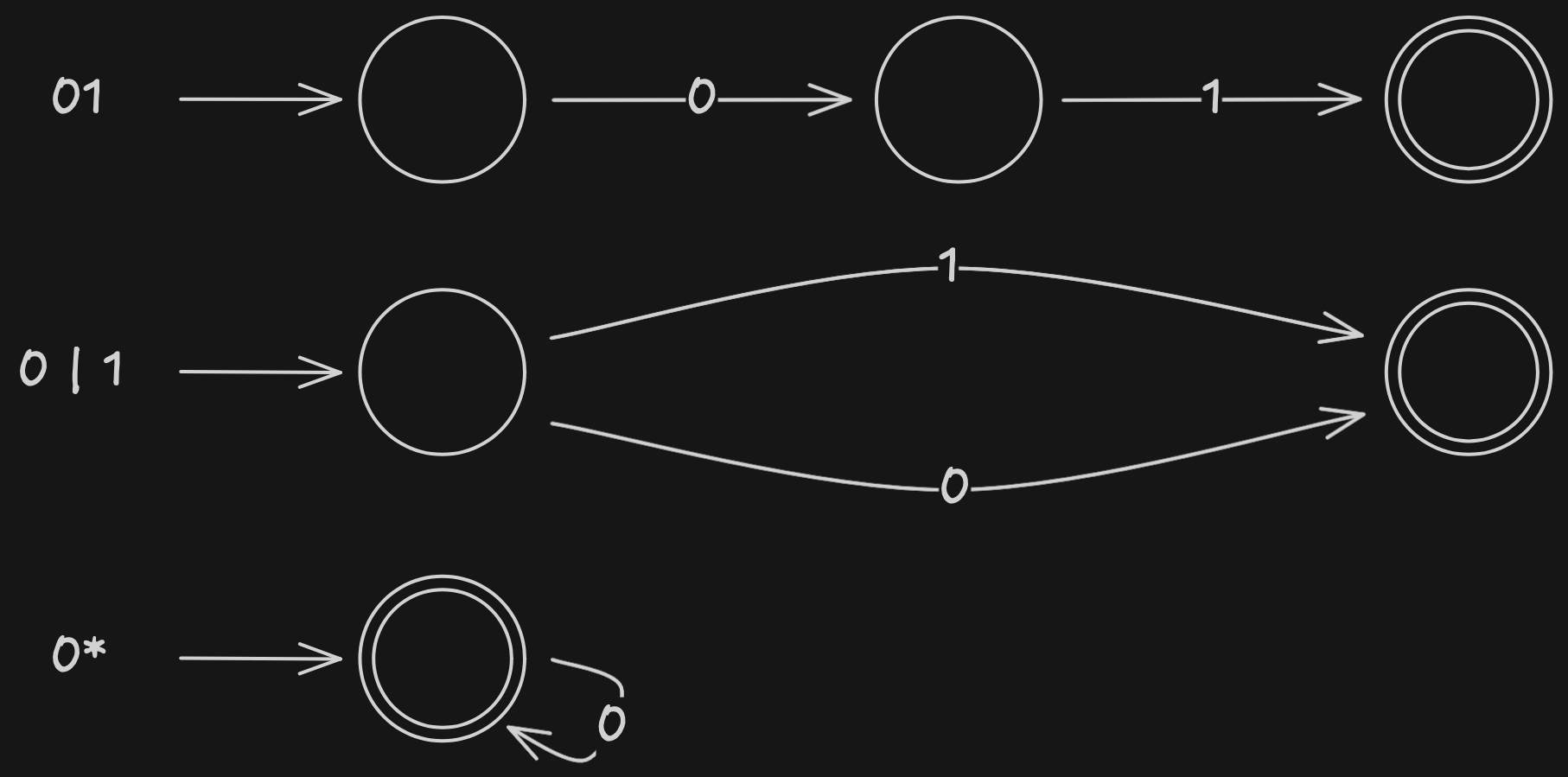
Ein regulärer Ausdruck lässt sich mit einem Syntaxdiagramm graphisch darstellen:

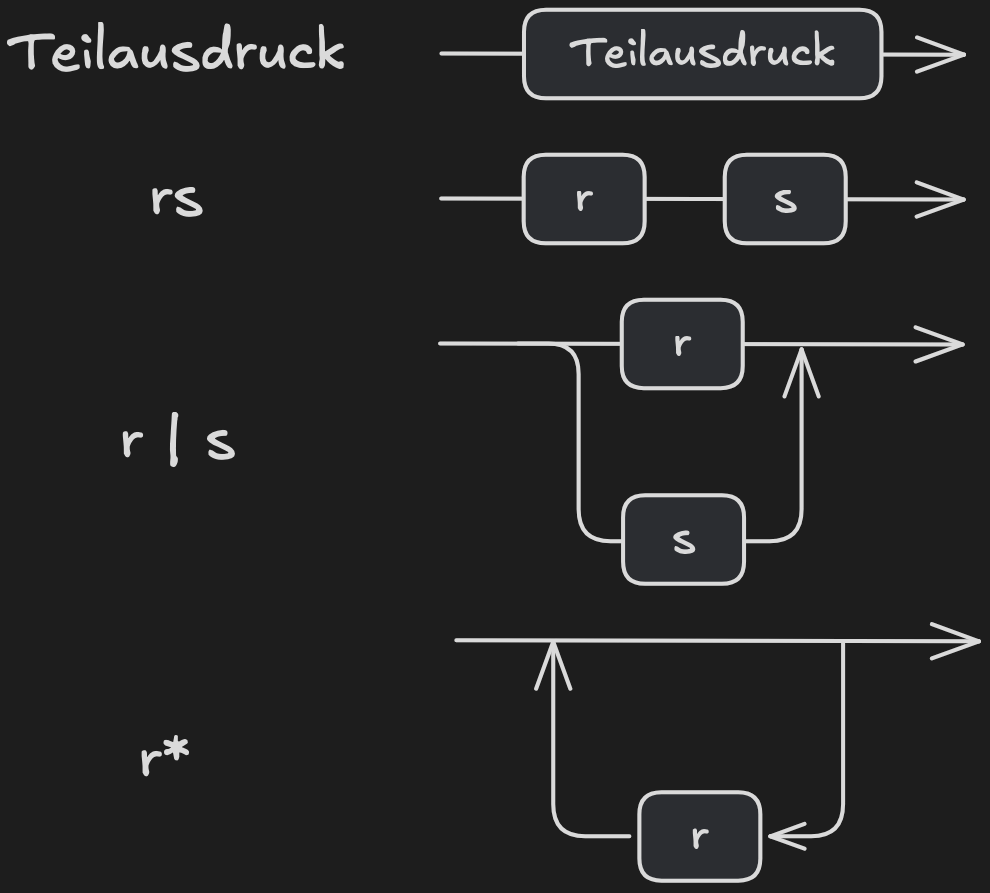
Lexikographische Ordnung

Beim Sortieren von Wörtern wird folgende Ordnung verwendet (angenommen, es gibt zwei Wörter $w_1$ und $w_2$):

1. $w_1<w_2$ falls $|w_1|<|w_2|$
2. Falls $|w_1|=|w_2|$: Nach Buchstaben innerhalb des Wortes ($baab<babb$)

Ableitungsbäume

Zu einer kontextfreien Grammatik kann ein Baum $t$ erstellt werden, der die Ableitung symbolisiert. Damit ein Baum als Ableitungsbaum bezeichnet werden darf, müssen folgende Bedingungen erfüllt sein:

• Die Wurzel muss mit $S$ markiert sein
• Jeder Knoten ist mit $X\in N\cup \Sigma \cup \{ϵ\}$ (einem (Nicht-) Terminal) markiert
• Jeder innere Knoten ist mit einem $A\in N$ (einem Nichtterminal) markiert
• Wenn ein innerer Knoten mit $A\in N$ (einem Nichtterminal) markiert ist und seine Nachfolger von links nach rechts mit $X_1,...X_n\in N\cup \Sigma \cup \{ϵ\}$ (einem Terminal), dann muss $A\to X_1...X_n\in P$ sein.
• Wenn ein Knoten $k$ mit $ϵ$ markiert ist, ist $k$ ein Blatt und der einzige Sohn seines Vaters

Ein Ableitungsbaum ist eine natürliche Beschreibung für die Ableitung einer bestimmten Satzform der Grammatik G, die man erhält, wenn man die Markierungen aller Blätter von links nach rechts liest. Diese Zeichenkette wird auch Front des Ableitungsbaumes genannt.

Ableitungsbaum für die Linksableitung

$$S\to aAS\to aSbAS\to aaabAS\to aabbaS\to aabbaa$$

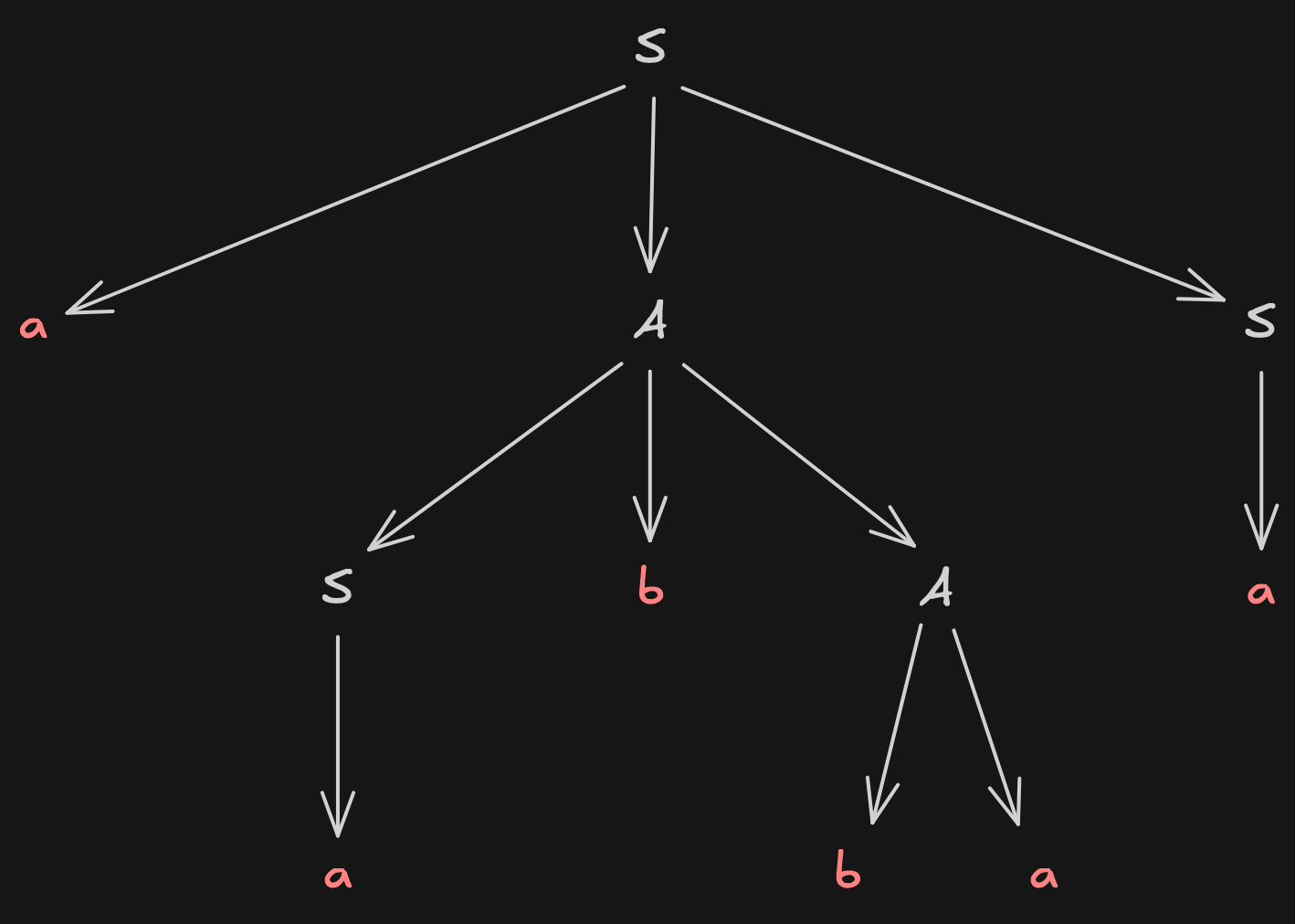
Pumping Lemma

Das Lemma dient als Negativ-Test, um per Widerspruch zu beweisen, dass eine Sprache nicht regulär ist. Es besagt: Jedes ausreichend lange Wort einer regulären Sprache enthält einen Teilbereich $y$ (eine nicht-leere Schleife), den man beliebig oft wiederholen („aufpumpen“) kann, ohne die Sprache zu verlassen: $x{y}^{i}z\in L$ Scheitert dies an einem Beispielwort, ist die Sprache nicht regulär.

Halteproblem der TM

Das Halteproblem ist unentscheidbar: Es existiert bewiesenermaßen (durch Diagonalisierung) kein Algorithmus, der für jede Turing-Maschine und Eingabe vorhersagen kann, ob sie stoppt oder endlos läuft. Es ist lediglich semi-entscheidbar, da man ein Anhalten zwar erkennen kann, eine Endlosschleife durch bloßes Simulieren jedoch nie sicher identifiziert wird.

LL(1)-Grammatiken, FIRST & FOLLOW

LL(1) steht für Lesen von links, Linksableitung und 1 Zeichen Vorschau (Lookahead). Damit eine Grammatik LL(1) ist, muss der Parser stets eindeutig ohne Raten entscheiden können, welche Regel gilt.

K.O.-Kriterien:

• Linksrekursion
• Gemeinsame Präfixe: Diese verletzen die Eigenschaft sofort, da sie die Eindeutigkeit zerstören.

FIRST- und FOLLOW-Mengen

Sie dienen der Konstruktion der Parsing-Tabelle.

• FIRST: Enthält alle möglichen Startzeichen einer Variablen (inklusive $ϵ$).
• FOLLOW: Enthält alle Zeichen, die im Wort direkt hinter der Variablen folgen können (niemals $ϵ$, oft das Endsymbol $$$).

Bedingung: Für LL(1) müssen die FIRST-Mengen alternativer Regeln disjunkt (überschneidungsfrei) sein.

Minimierung endlicher Automaten

Zum Minimieren von EAs kann folgender Algorithmus verwendet werden:

1. Stelle eine Tabelle aller Zustandspaare $(z,z^{\prime })$ von $M$ auf, mit $z$ ungleich $z^{\prime }$
2. Markiere alle Paare mit genau einem Endzustand
3. Für jedes unmarkierte Paar $(z,z^{\prime })$, teste für jedes Symbol $a$ ob $(z\to a,z^{\prime }\to a)$ markiert
   1. Falls ja, markiere auch $(z,z^{\prime })$
4. Wiederhole 3. bis sich keine Änderung mehr ergibt
5. Verschmelze alle unmarkierten Zustandspaare $(z,z^{\prime })$ zu einem neuen Zustand

Zuerst stellt man eine Tabelle auf, in der Angekreuzt wird, von welchem Zustand man welchen anderen Zustand erreichen kann. In den Zeilen wird der Startzustand weggelassen, in den Spalten der Endzustand:

	Z0	Z1	Z2	Z3	Z4
Z0	------	------	------	------	------
Z1		------	------	------	------
Z2			------	------	------
Z3				------	------
Z4					------

Dann werden alle Paare, bei denen genau einer der beiden ein akzeptierender Endzustand ist, markiert.

Als nächstes wird überprüft, was passiert, wenn bei jedem Zustand eines unmarkierten Zustandspaares die selbe Eingabe gemacht wird. Man erhält ein neues Paar $(z\stackrel{a}{\to }p,z^{\prime }\stackrel{a}{\to }{p}^{\prime })$. Wenn das neue Paar $(p,p^{\prime })$ bereits markiert ist, bedeutet das, dass nach Lesen des Symbols $a$ die Zustände in einen bereits bekannt unterschiedlichen Zustand übergehen. Man markiert $(z,z^{\prime })$.

Nachdem dies für den Rest der Tabelle wiederholt wurde, sind alle markierten Paare sicher verschieden. Alle unmarkierten Paare sind äquivalent und können kombiniert werden. Visuell kann man sich Vorstellen, dass die Kreise “übereinander geschoben werden”, da die Pfeile zu den jeweiligen Kreisen des Automaten für den neuen Kreis einfach kombiniert werden.

Vereinfachungen

Ziel bei der Vereinfachung ist, das Format der Produktionen einzuschränken, ohne deren Fähigkeit zur Erzeugung von Sprachen zu beschneiden. Eine kontextfreie Grammatik lässt sich durch folgende Maßnahmen vereinfachen:

• Eliminierung von ε-Regeln: Es gibt keine Produktionen der Form $A\to ϵ$ wenn $ϵ\notin L$
• Eliminieren nutzloser Symbole: Jede Variable und jedes Terminal von $G$ erscheint in der Ableitung mindestens eines Wortes aus $L$
• Eliminieren von Kettenregeln: Es gibt keine Produktionen der Form $A\to B$, wenn $A$ und $B$ Variablen sind

Eliminieren von ε-Regeln

1. Bestimme alle Nichtterminale, die in ein ε umgewandelt werden können: $N^{\prime }=\{A\in N\text{ | }A\to ϵ\}$
2. Bestimme alle Nichtterminale, aus denen das leere Wort ableitbar ist: $N^{\prime \prime }=\{A\in N\text{ | }A{\to }^{\ast }ϵ\}$
3. Für jede Regel, deren Rechte Seite ein Nichtterminal aus $N^{\prime \prime }$ enthält, fügen wir eine Regel ohne dieses Nichtterminal hinzu.
4. Eliminiere alle ε-Regeln (entferne das ε aus allen Umformungen und entferne die Umformung selbst, falls das ε nicht verodert ist)

Beispiel:

$S\to AB$, $A\to ϵ\text{ | }B$, $B\to b$

Hier führt $A$ zu einem leeren Wort, also “markieren” wir es im 1. Schritt. Da sich $A$ aus $S$ ableiten lässt, markieren wir auch dies. In Schritt 3 wird $S$ umgeformt, da wir das $A$ in der Ableitung dort markiert haben:

$S\to AB\text{ | }B$, $A\to ϵ\text{ | }B$, $B\to b$

Im letzten Schritt entfernen wir das ε aus der Ableitung von $A$:

$S\to AB\text{ | }B$, $A\to B$, $B\to b$

Eliminieren nutzloser Symbole

Beim Eliminieren von nutzlosen Symbolen wird darauf geachtet, welche Symbole nützlich für die Grammatik $G$ sind. Ein Symbol $X$ heißt nützlich, wenn mit seiner Hilfe mindestens ein Terminalwort erzeugt werden kann, also wenn gilt:

$$S{\to }^{\ast }\alpha X\beta {\to }^{\ast }w$$

mit $\alpha ,\beta \in (N\cup \Sigma {)}^{\ast }$ und $w\in {\Sigma }^{\ast }$.

Beim Eliminieren von nützlichen Symbolen wird also darauf geachtet, dass zwei Aspekte der Nützlichkeit für jedes Symbol gegeben sind:

1. Aus $X$ muss eine Terminalzeichenkette ableitbar sein (Lemma 1)
2. $X$ muss Teil einer Zeichenkette sein, die aus $S$ ableitbar ist (Lemma 2)

Lemma 1 beschäftigt sich mit der Erreichbarkeit von Symbolen. Ein Symbol muss erreichbar sein, also vom Startsymbol aus in einer Folge von Produktionen irgendwann erzeugt werden. Bei Lemma 1 werden alle Symbole, die niemals vom Startsymbol aus erreicht werden können, eliminiert. Der Algorithmus hierzu sieht so aus:

1. Merke dir alle Nichtterminale, die per Ableitung in ein Terminal verwandelt werden können ($N_2=\{A\text{ | }A\to w\text{ fu¨r ein }w\in {\Sigma }^{\ast }\}$ ⇒ A muss ein Nichtterminal produzieren, was in der Menge aller Wörter steht)
2. Prüfe, welche Ableitungen zu den gemerkten Nichtterminalen führen, und markiere diese, bis alle Ableitungen durchlaufen sind. Sobald alle anderen Ableitungen angeschaut und markiert sind, entferne alle nicht markierten Ableitungen.

Lemma 2 hingegen eliminiert nicht erzeugende Symbole. Ein Symbol ist erzeugend, wenn es ein Wort bestehend aus nur Terminalsymbolen ableiten kann. Alle Symbole, die kein terminales Wort erzeugen können, sind ebenfalls nutzlos.

1. Starte bei $S$ und durchlaufe alle möglichen Ableitungen, um zu sehen, welche Nichtterminale erreicht werden können. Entferne alle Ableitungen, die nicht erreicht werden können.

Eliminieren von Kettenregeln

Kettenregeln tragen zur Erzeugung eines Wortes nichts bei. Sie haben folgende Form und können durch drei Schritte eliminiert werden:

$$A\to B\text{ mit }A,B\in N$$

1. Entfernen von Zyklen: Gibt es Nichtterminale, die einen Zyklus erzeugen (z.B. $A_1\to A_2\to A_3\to A_1$), fügen wir ein neues Nichtterminal $A$ hinzu und ersetzen alle $A_i$ durch $A$.
2. Umnummerierung: $N$ hat nun $n$ Elemente. Wir bezeichen diese mit $A_1,...,A_n$, so dass gilt: Wenn $A_i\to A_j$, dann ist $i<j$
3. Ersetzen von Kettenregeln: Wenn noch Regeln wie $A_i\to A_j$ dann kann jede Regel $A_j\to w$ ersetzt werden durch $A_i\to w$

Chomsky-Normalform (CNF)

Eine kontextfreie Grammatik ist in CNF, wenn alle ihre Produktionen eine der folgenden Formen haben:

1. $A\to BC$
2. $A\to a$
3. $A\to ϵ$ (nur vorhanden, wenn $G$ das leere Wort erzeugt)

(mit $A,B,C,S\in N$ und $a\in \Sigma$)

⇒ Zu jeder kontextfreien Sprache $L$ lässt sich eine Grammatik $G$ in CNF angeben, so dass $L(G)=L$ ist.

Zum Erzeugen der CNF einer Grammatik muss die Grammatik maximal vereinfacht vorliegen. Man beachte die Produktionen $A\to X_1{X}_2...X_m$:

• Wenn $X_i=a\in \Sigma$ vorhanden ist: Ersetze $X_i$ durch $C_a$, füge neue Produktion $C_a\to a$ hinzu, ersetze alle anderen $a$ durch $C_a$.
• Wenn kein $X_i=a\in \Sigma$ vorhanden ist: Betrachte die Produktion $A\to B_1{B}_2...B_m$ und ersetze dies durch die Produktionen $A\to B_1{D}_1,D_1\to B_2{D}_2,...,D_{m-2}\to B_{m-1}{B}_m$.

Wortproblem & CYK-Algorithmus

Wenn eine kontextfreie Grammatik $G$ in der CNF sowie ein Wort $w$ gegeben sind, stellt sich die Frage, ob das Wort $w$ Teil der Sprache $L(G)$ ist ($w\in L(G)$). Dies kann mit dem Cocke-Younger-Kasami-Algorithmus (CYK) beantwortet werden.

Die Idee lautet wiefolgt: Für jedes Teilwort $w$ der Sprache $L$ wird die Menge der Nichtterminale berechnet, die benötigt werden, um das Wort zu erzeugen. Man dringt hierbei von kleineren zu immer größeren Teilwörtern vor. Am Einfachsten ist dies Tabellarisch zu erreichen.

Beispiel

• Gesuchtes Wort $w=bbabaa$
• Produktionen: $S\to AB\text{ | }BC$, $A\to BA\text{ | }a$, $B\to CC\text{ | }b$, $C\to AB\text{ | }a$

Es wird eine Tabelle mit $n$ Zeilen und $n$ Spalten aufgestellt, wobei $n=|w|$:

$V_{i,j}$	1	2	3	4	5	6
1
2	------
3	------	------
4	------	------	------
5	------	------	------	------
6	------	------	------	------	------

Entlang der Hauptdiagonalen werden dann die Terminale von $w$ eingetragen. Dann werden die Terminale durch die möglichen Nichtterminale, durch die sie direkt erzeugt werden können ersetzt:

$V_{i,j}$	1	2	3	4	5	6
1	B
2	------	B
3	------	------	A, C
4	------	------	------	B
5	------	------	------	------	A, C
6	------	------	------	------	------	A, C

Hier beginnt der Algorithmus. Zuerst schauen wir uns $V_{1,2}$ an. Da es keine Produktion gibt, die $BB$ erzeugt, tragen wir ”{}” ein:

$V_{i,j}$	1	2	3	4	5	6
1	B	{}
2	------	B
3	------	------	A, C
4	------	------	------	B
5	------	------	------	------	A, C
6	------	------	------	------	------	A, C

Bei $V_{2,3}$ hingegen gibt es Produktionen, die entweder $BA$ oder $BC$ erzeugen, weshalb wir die Terminale für die Produktionen ($S,A$) dort eintragen. Weiter geht es danach mit $V_{1,3}$, $V_{3,4}$, $V_{2,4}$, $V_{1,4}$, $V_{4,5}$, $V_{3,5}$ usw.

Nachdem die Tabelle gefüllt ist, muss in der oberen rechten Ecke das Startsymbol $S$ zu finden sein. Falls es vorhanden ist, ist das Wort $w$ in der Sprache $L(G)$ enthalten.