Klausurthemen

Formale Systeme

Post’sche Produktionssysteme

Ein Post’sches Produktionssystem ist eine spezielle Art von formalem System. Sie bestehen aus einem Axiom, d.h. einer bestimmten Kombination von Zeichen, die als gegeben angenommen werden und einer Menge von Regeln, die bestimmt, in welche Zeichenfolge eine gegebene Zeichenfolge umgewandelt werden kann. Die durch die Regeln aus dem Axiom erzeugbaren Zeichenketten nennt man Sätze des Produktionssystems.

Beispiel:

Axiom: $AO$ Regeln:

• $Ax\Rightarrow AIIx$
• $xO\Rightarrow xIIO$
• $xIy\Rightarrow xIIIy$
• $xIIy=>xy$

Im genannten Beispiel stehen $A$, $I$ und $O$ für Symbole aus dem System, während die Zeichen $x$ und $y$ für Variablen stehen, die durch beliebige Zeichenketten aus dem System ausgetauscht werden können. $A$, $I$ und $O$ werden hierbei Terminale, $x$ und $y$ Nichtterminale genannt (“Terminal” → $A$, $I$ und $O$ können nicht mehr ersetzt werden).

Endliche Automaten

Endliche Automaten können als “Black Box” betrachtet werden, die sich aufgrund einer Folge von Eingaben in einem bestimmten Zustand befindet. Je nach aktuellem Zustand und Eingabe geht der endliche Automat (EA) in einen weiteren Folgezustand über. Der EA besitzt zudem einen oder mehrere ausgezeichnete Zustände (Endzustände). Wenn der endliche Automat nach einer Folge von Eingaben einen Endzustand erreicht, wird diese Eingabe vom Automaten akzeptiert.

Zustandsdiagramm

Einen EA kann auch visuell dargestellt werden. Ein Zustandsdiagramm für einen Automaten, der den Eintritt in einem Schwimmbad kontrolliert, sieht so aus:

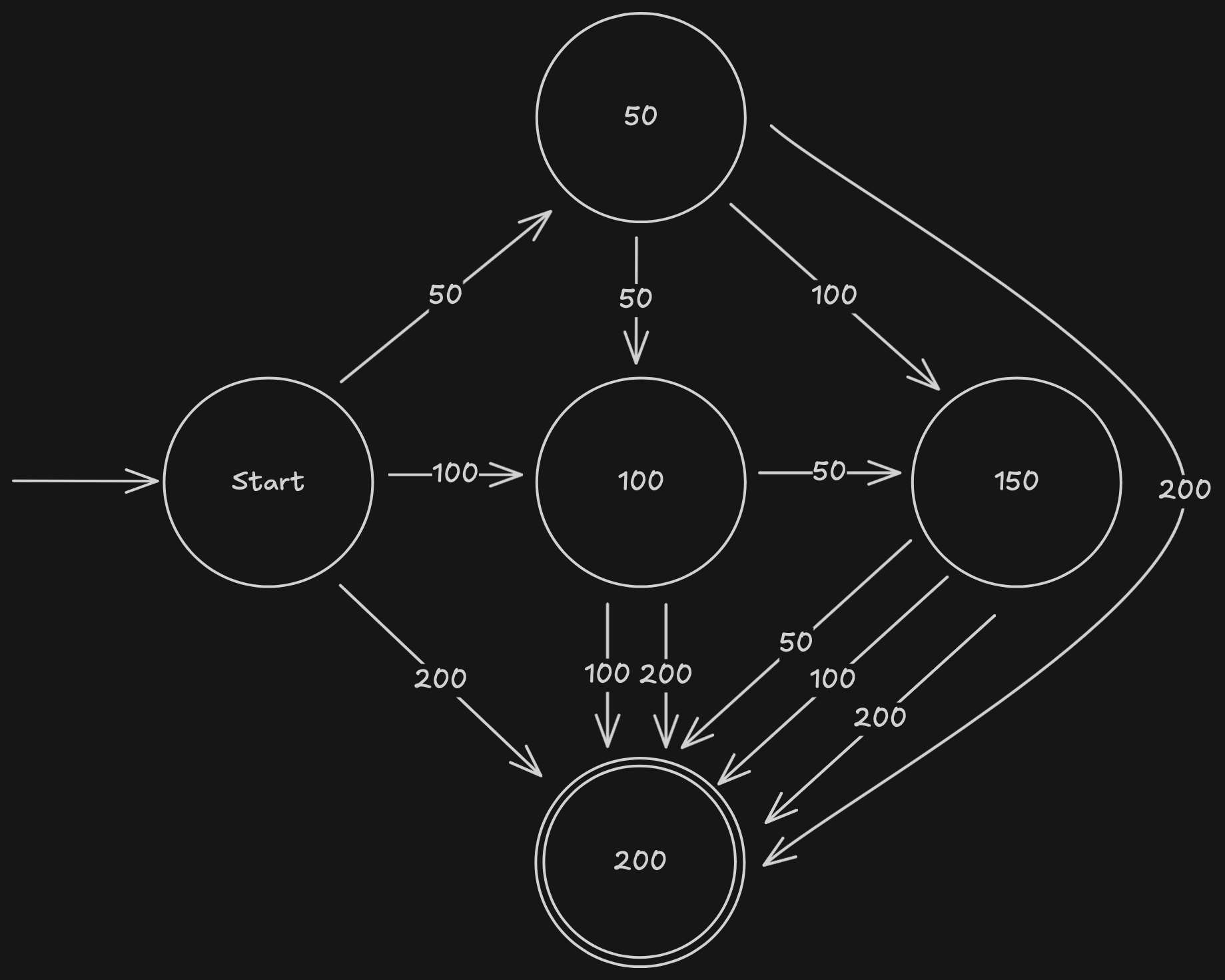
Hierbei kostet der Eintritt 2€. Der Automat akzeptiert 50 Cent sowie 1€- und 2€-Münzen. Sobald mindestens 2€ eingeworfen sind, öffnet der Automat das Drehkreuz (befindet sich in einem akzeptierenden Endzustand).

Die Zustände des Automaten sind als Kreise dargestellt. Die Übergänge zwischen den Kreisen sind die Pfeile, die Eingaben, die zum Übergang führen, sind die Symbole an den Pfeilen. Der Startzustand ist der Kreis mit dem Eingangspfeil, der Endzustand der Doppelkreis.

Formale Definition

Ein EA kann definiert werden durch:

$$EA=(Q,\Sigma ,\delta ,q_0,F)$$

Die Symbole stehen für:

• $Q$: Endliche Menge von Zuständen
• $\Sigma$: Endliches Eingabealphabet
• $\delta$: Die Übergangsfunktion $\delta :(Q\times E)\to Q$
• $q_0$: Der Anfangszustand
• $F$: Die Menge der akzeptierenden Endzustände

Die Eingabe der Übergangsfunktion $\delta$ ist ein Paar bestehend aus dem aktuellen Zustand $q\in Q$ und dem gelesenen Symbol $a\in \Sigma$. Die Ausgabe ist genau ein Folgezustand $q^{\prime }\in Q$.

EAs mit Ausgabe

Bei endlichen Automaten mit Ausgabe gibt es zwei Möglichkeiten, diesen Auszugeben: Mit dem erreichten Zustand und mit dem durchgeführten Übergang.

Moore-Automat

Bei einem Moore-Automat wird beim Erreichen eines Zustands eine Ausgabe gemacht. Er kann definiert werden als:

$$\text{Moore-EA}=(Q,\Sigma ,\Delta ,\delta ,\lambda ,q_0)$$

Wobei:

• $Q$: Endliche Menge von Zuständen
• $\Sigma$: Endliches Eingabealphabet
• $\Delta$: Endliches Ausgabealphabet
• $\delta$: Die Übergangsfunktion $\delta :(Q\times E)\to Q$
• $\lambda$: Die Ausgabefunktion $\lambda :Q\to \Delta$
• $q_0$: Der Anfangszustand

Mealy-Automat

Der Mealy-Automat hingegen macht eine Ausgabe, wenn ein Übergang durchlaufen wird. Er kann definiert werden als:

$$\text{Mealy-EA}=(Q,\Sigma ,\Delta ,\delta ,\lambda ,q_0)$$

Wobei:

• $Q$: Endliche Menge von Zuständen
• $\Sigma$: Endliches Eingabealphabet
• $\Delta$: Endliches Ausgabealphabet
• $\delta$: Die Übergangsfunktion $\delta :(Q\times E)\to Q$
• $\lambda$: Die Ausgabefunktion $\lambda :\underline{(Q\times \Sigma )}\to \Delta$
• $q_0$: Der Anfangszustand

Die Mealy- und Moore-Automaten unterscheiden sich ausschließlich darin, dass der Moore-Automat technisch gesehen bereits im Startzustand eine Ausgabe macht. Anderweitig sind sie equivalent. Zu jedem Moore-/Mealy-EA findet man einen Mealy-/Moore-EA, der für alle Eingabeketten $w$ dieselbe Ausgabe liefert (insofern die Ausgabe des Startzustandes vernachlässigt wird).

(Fehlend hier: Zeichnungen)

Beispiel zu einem Mealy-Automat zur Berechnung des Modulo 3:

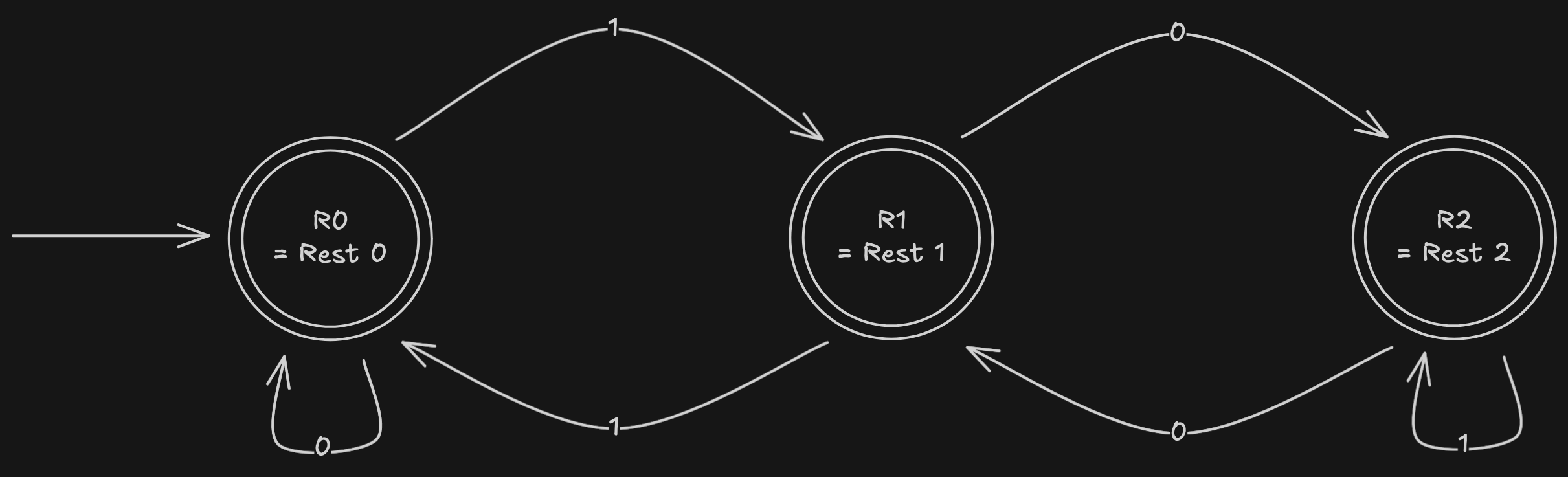
Akzeptierte Folgen

Wenn eine Eingabe komplett gelesen ist und der Zustandsspeicher einen Endzustand enthält ist die Zeichenfolge akzeptiert.

Alphabete, Wörter und Sprachen

Symbole

Die bisherigen Eingaben für z.B. den Eintrittsautomaten (50, 100, 200) waren atomare Symbole für Geldstücke. Der Lesekopf liest das Eingabeband symbolweise. Die Eingabesymbole zusammen ergeben ein Eingabewort. Man kann Symbole auch Buchstaben nennen.

Alphabete

Die Menge der möglichen Eingabesymbole bildet das Eingabealphabet. Formal wird meist $\Sigma$ verwendet, also:

$$\Sigma =\{50,100,200\}$$

Allgemein können die Symbole $a_1$ bis $a_n$ verwendet werden:

$$\Sigma =\{a_1,a_2,...,a_n\}$$

Wörter

Die endlich langen Zeichenfolgen, die über einem Alphabet $\Sigma$ gebildet werden können, heißen Wörter über $\Sigma$. Sie werden durch die Aneinanderreihung von Symbolen oder bereits existierenden Wörtern erzeugt.

Wörter können:

• Konkateniert werden (aneinandergereiht werden)
• Potenziert werden ($w^0=ϵ$, $w^i=w{w}^{i-1}$)
• Umgekehrt werden ($w^R=w$ (Wort wird rückwärts gelesen))

Die Menge aller Wörter über $\Sigma$ wird ${\Sigma }^{\ast }$ geschrieben:

• Jeder Buchstabe $a\in \Sigma$ ist auch ein Wort über $\Sigma$, also $a\in {\Sigma }^{\ast }$
• Sind $v,w\in {\Sigma }^{\ast }$, so ist auch $vw\in {\Sigma }^{\ast }$
• $ϵ$ ist das leere Wort über jedem Alphabet $\Sigma$. Es gilt $wϵ=ϵw=w$

Beispiel:

$$\Sigma =\{a,b\}$$ $${\Sigma }^{\ast }=\{ϵ,a,b,ab,ba,bb,aaa,aab,aba,baa,abb,bba,bbb,...\}$$

Außerdem kann die Länge eines Wortes mit $|w|$ bezeichnet werden:

$$|a|=1$$ $$|ϵ|=0$$ $$|abc|=3$$

Aber Obacht! Es geht immer um die Länge der Symbole, nicht der Zeichen/Ziffern. Beim Eintrittsautomaten beispielsweise gilt:

$$|50|=1$$

Lexikographische Ordnung

Beim Sortieren von Wörtern wird folgende Ordnung verwendet (angenommen, es gibt zwei Wörter $w_1$ und $w_2$):

1. $w_1<w_2$ falls $|w_1|<|w_2|$
2. Falls $|w_1|=|w_2|$: Nach Buchstaben innerhalb des Wortes ($baab<babb$)

Sprachen

Eine Sprache $L$ über einem Alphabet $\Sigma$ ist eine Menge von Wörtern über $\Sigma$. L ist also eine Teilmenge von $E^{\ast }$ ($L\subseteq {\Sigma }^{\ast }$).

Folgende Operationen können auf Sprachen ausgeführt werden:

• Konkatenation: $LM=\{vw|v\in L\vee w\in M\}$
• Potenz: $L^0=ϵ$, $L^i=L{L}^{i-1}$
• Reverse: $L^R=\{w^R|w\in L\}$

Kleensche & positive Hülle

Die Kleensche Hülle eines Alphabets $\Sigma$ oder einer formalen Sprache $L$ ist die Menge aller Wörter, die durch beliebige Konkatenation von Symbolen des Alphabets $\Sigma$ bzw. von Wörtern der Sprache $L$ gebildet werden können, wobei das leere Wort $ϵ$ inbegriffen ist. Die positive Hülle hingegen enthält das leere Wort nur dann, wenn die Sprache selbst das leere Wort beinhaltet. Wenn also $ϵ\in L^{+}$, ist auch $ϵ\in L$

Reguläre Ausdrücke & Grammatiken

Die von endlichen Automaten akzeptierten Sprachen lassen sich durch einfache Ausdrücke beschreiben, die man als regulären Ausdrücke bezeichnet.

Die Menge $\text{Reg}(\Sigma )$ der regulären Ausdrücke (über dem Alphabet $\Sigma$) ist definiert durch:

1. $\varnothing$ ist ein regulärer Ausdruck
2. $ϵ$ ist ein regulärer Ausdruck
3. Für jedes $a\in \Sigma$ ist $a$ ein regulärer Ausdruck
4. Sind $r$ und $s$ reguläre Ausdrücke, so auch
   1. $r|s$ → Vereinigung
   2. $rs$ → Konkatenation
   3. $r^{\ast }$ → Kleene Stern

Falls nicht geklammert ist gilt ${}^{\ast }$ vor $rs$ und $rs$ vor |.

Semantik regulärer Ausdrücke

Ein regulärer Ausdruck $r$ stellt eine Sprache $L(r)$ wie folgt dar:

• $L(\varnothing )=\{\}$
• $L(ϵ)=\{ϵ\}$
• $L(a)=\{a\}$ für alle $a\in \Sigma$
• $L(r|s)=L(r)\cup L(s)$
• $L(rs)=L(r)L(s)$
• $L(r^{\ast })=L(r{)}^{\ast }=L^0\cup L^1\cup L^2\cup \text{...}$

Beispiele

• a → Einfaches Symbol: a 1x gematched
• (a|b) → a oder b wird 1x gematched
• ab → ab wird 1x gematched
• a* → a wird 0-mal bis ∞-mal gematched
• a+ → a wird 1-mal bis ∞-mal gematched
• (a|b)* → a oder b wird 0-mal bis ∞-mal gematched (jegliche Kombination aus a und b, da sich der Kleene Stern auf die Klammer bezieht)
• ab* → a wird 1x gematched, b wird 0-mal bis ∞-mal gematched
• (ab) → ab wird 1-mal bis ∞-mal gematched (abababab...)
• aa* | bb* → Erst wird ein einzelnes a gematched, dann 0 bis ∞-viele a’s oder ein b, dann 0 bis ∞-viele b’s

Experimentieren mit regulären Ausdrücken

Auf der Seite regex101.com kann man gut mit regulären Ausdrücken experimentieren. Mithilfe der Seite können Texte auf reguläre Ausdrücke überprüft werden!

Reguläre Ausdrücke und endliche Automaten

Zu jedem regulären Ausdruck gibt es einen endlichen Automaten, den man aus dem regulären Ausdruck hinaus erschließen kann.

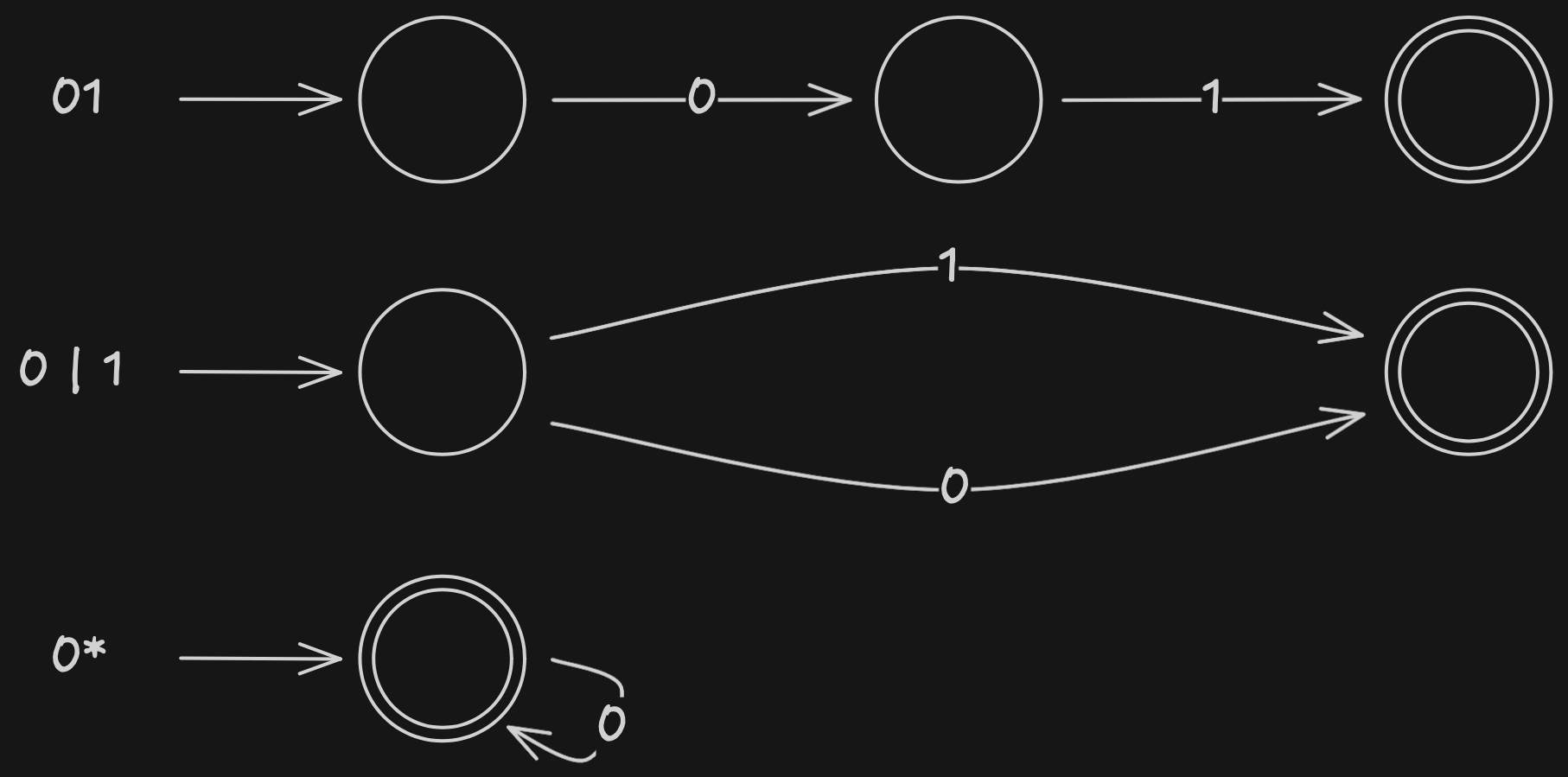
Es ist auch möglich, die Automaten zwei regulärer Ausdrücke zu verknüpfen. Formell wird dies mit dem leeren Wort gemacht:

Das leere Zeichen kann dann in einem zweiten Schritt entfernt werden:

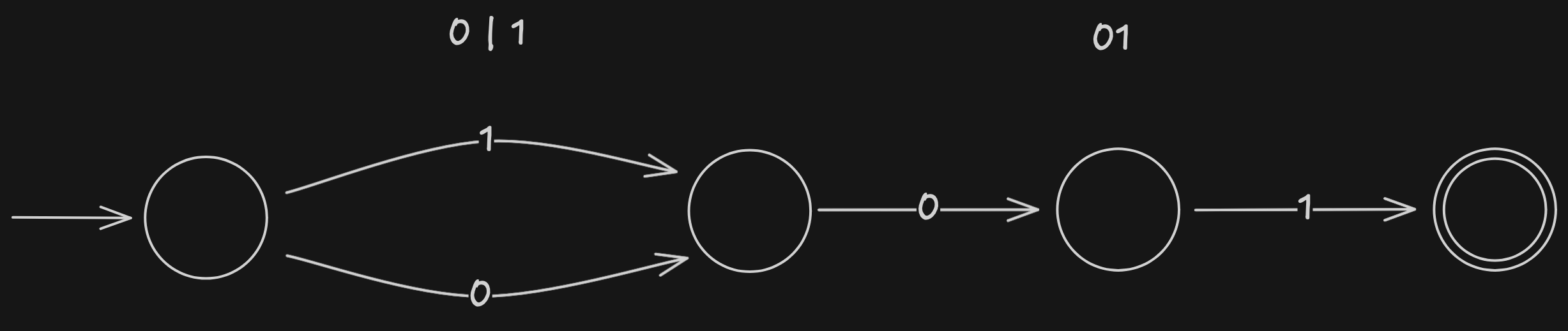
Beim Konstruieren dieser Automaten ist es wichtig, darauf zu achten, dass leere Wörter immer eliminiert werden.

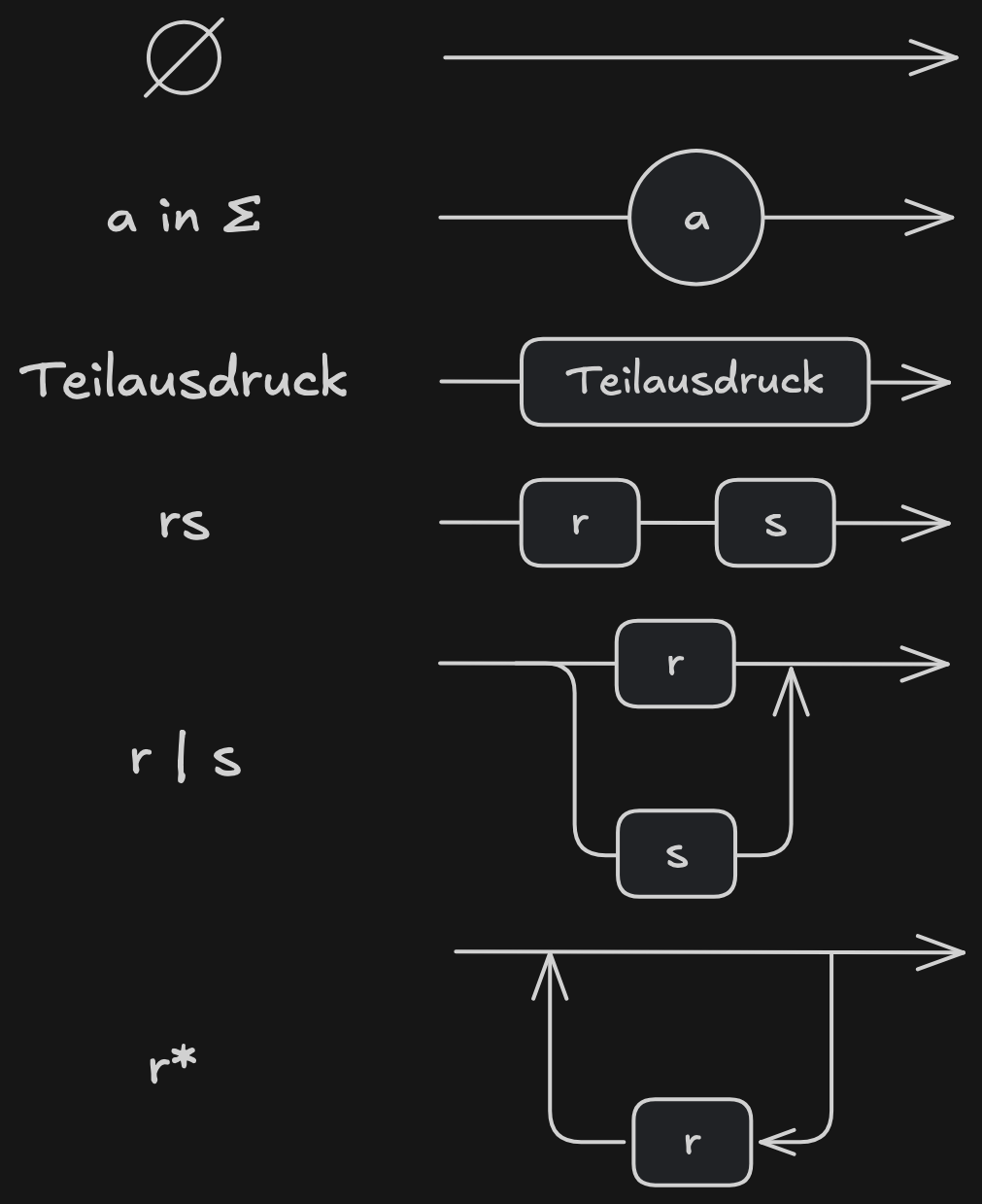
Syntaxdiagramme

Ein regulärer Ausdruck lässt sich mit einem Syntaxdiagramm graphisch darstellen:

Minimierung endlicher Automaten

Zum Minimieren von EAs kann folgender Algorithmus verwendet werden:

1. Stelle eine Tabelle aller Zustandspaare $(z,z^{\prime })$ von $M$ auf, mit $z$ ungleich $z^{\prime }$
2. Markiere alle Paare mit genau einem Endzustand
3. Für jedes unmarkierte Paar $(z,z^{\prime })$, teste für jedes Symbol $a$ ob $(z\to a,z^{\prime }\to a)$ markiert
   1. Falls ja, markiere auch $(z,z^{\prime })$
4. Wiederhole 3. bis sich keine Änderung mehr ergibt
5. Verschmelze alle unmarkierten Zustandspaare $(z,z^{\prime })$ zu einem neuen Zustand

Zuerst stellt man eine Tabelle auf, in der Angekreuzt wird, von welchem Zustand man welchen anderen Zustand erreichen kann. In den Zeilen wird der Startzustand weggelassen, in den Spalten der Endzustand:

	Z0	Z1	Z2	Z3	Z4
Z0	------	------	------	------	------
Z1		------	------	------	------
Z2			------	------	------
Z3				------	------
Z4					------

Dann werden alle Paare, bei denen einer der beiden ein akzeptierender Endzustand ist, markiert:

	Z0	Z1	Z2	Z3	Z4
Z0	------	------	------	------	------
Z1		------	------	------	------
Z2			------	------	------
Z3				------	------
Z4	x	x	x	x	------

Als nächstes wird überprüft, was passiert, wenn bei jedem Zustand eines unmarkierten Zustandspaares die selbe Eingabe gemacht wird. Man erhält ein neues Paar $(z\stackrel{a}{\to }p,z^{\prime }\stackrel{a}{\to }p)$. Wenn das neue Paar $(p,p^{\prime })$ bereits markiert ist, bedeutet das, dass nach Lesen des Symbols a die Zustände in einen bereits bekannt unterschiedlichen Zustand übergehen. Man markiert $(z,z^{\prime })$.

	Z0	Z1	Z2	Z3	Z4
Z0	------	------	------	------	------
Z1	x	------	------	------	------
Z2		x	------	------	------
Z3	x		x	------	------
Z4	x	x	x	x	------

Nachdem dies für den Rest der Tabelle wiederholt wurde, sind alle markierten Paare sicher verschieden. Alle unmarkierten Paare sind äquivalent und können kombiniert werden. Hier wird aus $(z_2,z_0)$ ein neuer Zustand $z_{20}$ und aus $(z_3,z_1)$ wird $z_{31}$, da beide bei den selben Eingaben gleich reagieren. Visuell kann man sich Vorstellen, dass die Kreise “übereinander geschoben werden”, da die Pfeile zu den jeweiligen Kreisen des Automaten für den neuen Kreis einfach kombiniert werden.

Nichtdeterministische endliche Automaten (NEA)

Ein nichtdeterministischer endlicher Automat (NEA) ist ein Automat, bei dem aus einem Anfangszustand mit einer Eingabe mehrere Zustände erreicht werden können. Es ist also nicht eindeutig festgelegt, in welchem der passenden Zustände man landet. Ein NEA kann sozusagen also “hellsehen”, d.h. er weiß immer, welcher der möglichen Wege zu wählen ist (eigentlich macht das ein Backtracking-Algorithmus, aber egal).

Ein NEA wird formell definiert durch

$$\text{NEA}=(Q,\Sigma ,\delta ,q_0,F)$$

wobei:

• $Q$ die endliche Menge von Zuständen darstellt
• $\Sigma$ für das endliche Eingabealphabet steht
• $\delta$ die Übergangsrelation $\delta :(Q\times \Sigma )\to Q$ symbolisiert
• $q_0$ der Anfangszustand ist
• $F$ die Menge der akzeptierenden Endzustände verkörpert

Umformung NEA zu DEA

Jeder NEA lässt sich durch die Potenzmengenkonstruktion auch in einen DEA umstrukturieren. Dabei wird angenommen, dass ein Zustand des DEA alle Zustände, in denen sich der NEA nach einer Eingabe befinden könnte, kodiert. Die Zustandsmenge des DEA ist dabei Teil der Potenzmenge der Zustandsmenge des NEA - daher der Name. (Problem: DEAs, die auf diese Art konstruiert werden, werden meist sehr groß.)

Bei der Potenzmengenkonstruktion wird ein DEA

$$\text{DEA}=(Q^{\prime },\Sigma ,{\delta }^{\prime },q_o^{\prime },F^{\prime })$$

zu einem NEA

$$\text{NEA}=(Q,\Sigma ,\delta ,q_0,F)$$

aufgebaut:

1. Die Zustandsmenge $Q^{\prime }$ und die Menge der akzeptierenden Endzustände $F^{\prime }$ werden als leere Mengen gewählt.
2. $q_0^{\prime }=\{q_0\}$. Füge $q_0^{\prime }$ zu $Q^{\prime }$ hinzu.
3. Konstruiere den Folgezustand $q^{\prime \prime }$ für alle $q^{\prime }$ aus $Q^{\prime }$ und für alle $s$ aus $\Sigma$ als Menge aller Zustände, die der NEA in dieser Situation erreichen könnte.
4. Füge $q^{\prime \prime }$ zu $Q^{\prime }$ hinzu, falls noch nicht enthalten
5. Ergänze die Übergangsfunktion ${\delta }^{\prime }:(q^{\prime },s)=q^{\prime \prime }$
6. Wiederhole Schritt 3 bis 5, bis sich $Q^{\prime }$ und ${\delta }^{\prime }$ nicht mehr ändern
7. Wähle die Menge der Finalzustände $F^{\prime }$ als diejenige Teilmenge von $Q^{\prime }$, deren Zustände einen Finalzustand aus $F$ enthalten.

⇒ Der DEA kann am ende bis zu $2^n$ Zustände haben!

Beispiel

NEA:

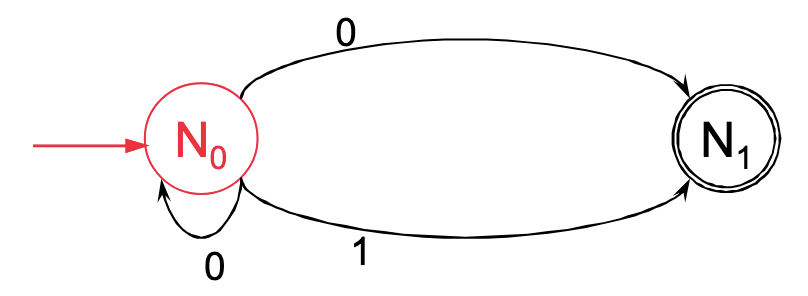
Als erstes wird für der Startzustand $q_0^{\prime }$ als $\{q_0\}$ übernommen:

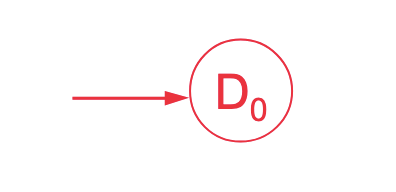
Bei Eingabe $0$ zum Zustand $N_0$ würde der NEA zwischen $N_1$ und $N_0$ entscheiden müssen. Beim DEA wird dafür ein neuer Zustand $D_{10}$ erstellt:

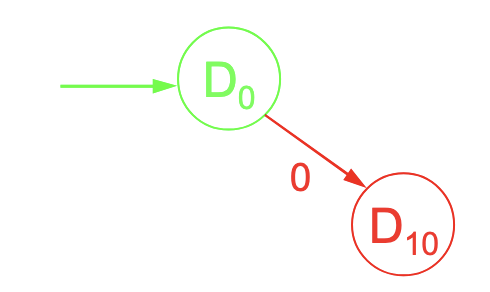
Bei Eingabe $1$ hingegen wechselt der NEA zu $N_1$. Dieses Verhalten wird als $D_1$ übernommen:

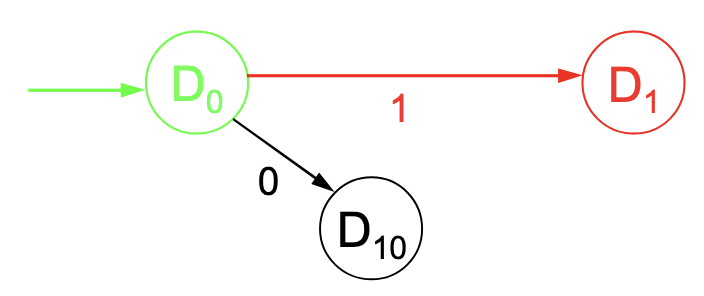
Nun ist jedoch bei $D_{10}$ die Eingabe einer $0$ nicht Eindeutig, deswegen benötigen wir eine weitere Schleife (schließlich wissen wir nicht, ob wir uns in $N_0$ oder $N_1$ befinden, solange wir in $D_{1}0$ sind):

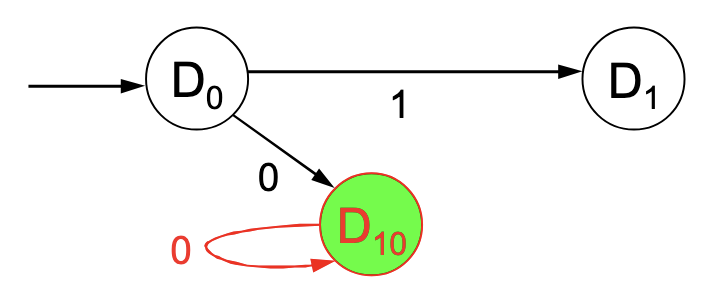
Zu guter Letzt wird die Eingabe $1$ im “Quantenzustand” $D_{10}$ eingebaut:

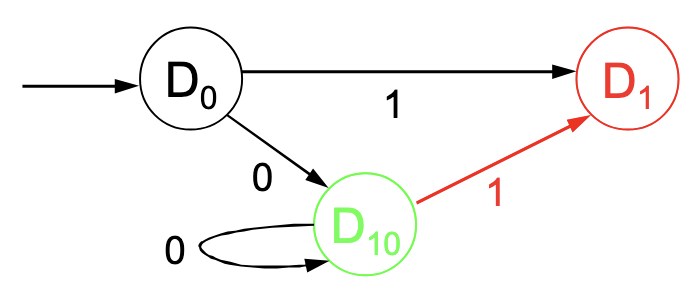
Da nun alle Übergange eingebaut sind, können die Endzustände gewählt werden:

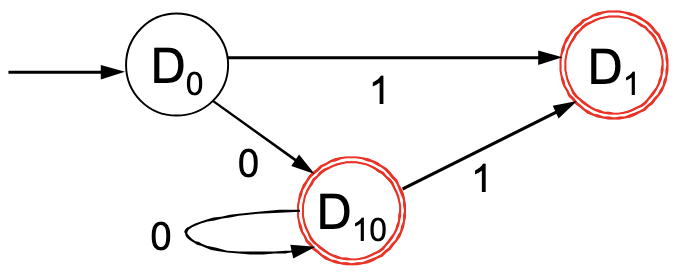
In tabellarischer Darstellung sieht dieser Algorithmus folgendermaßen aus:

Von ($D_n$ = $N_n$ / $\text{Eingabe}$)	NEA	DEA
Start	$N_0$	$D_0$
$D_0$ = $N_0$ / $0$	$N_0$ / $N_1$	$D_{10}$
$D_0$ = $N_0$ / $1$	$N_1$	$D_1$
$D_{10}=\{N_0,N_1\}$ / $0$	$N_0$ / $N_1$	$D_{10}$
$D_{10}=\{N_0,N_1\}$ / $1$	$N_1$	$D_1$

Regulärer Ausdruck aus NEA

Mit der Zustandselimination kann aus einem NEA ein regulärer Ausdruck erzeugt werden. Die Zustandselimination verwendet sog. verallgemeinerte NEAs (VNEAs), um den regulären Ausdrück möglichst einfach zu erreichen (links ist ein NEA, rechts ein VNEA):

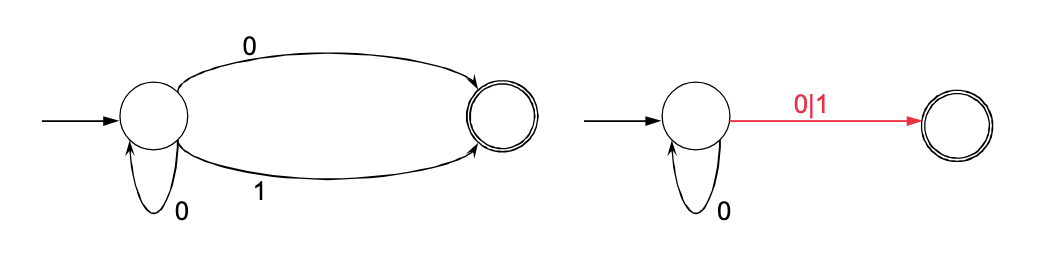
Bei der Zustandselimination wird folgendes gemacht:

1. Wandle den NEA in einen VNEA um
2. Wiederhole für alle Endzustände $q\in F$:
   1. Eliminiere (iterativ, also nacheinander, nicht gleichzeitig!) alle Zustände außer dem Startzustand $q_0$ und $q$.
   2. Bilde einen regulären Ausdruck aus dem finalen Automaten
3. Vereinige die Ausdrücke für alle Endzustände q
   1. Bilde die Summe aller entstandenen regulären Ausdrücke

Beispiel

NEA:

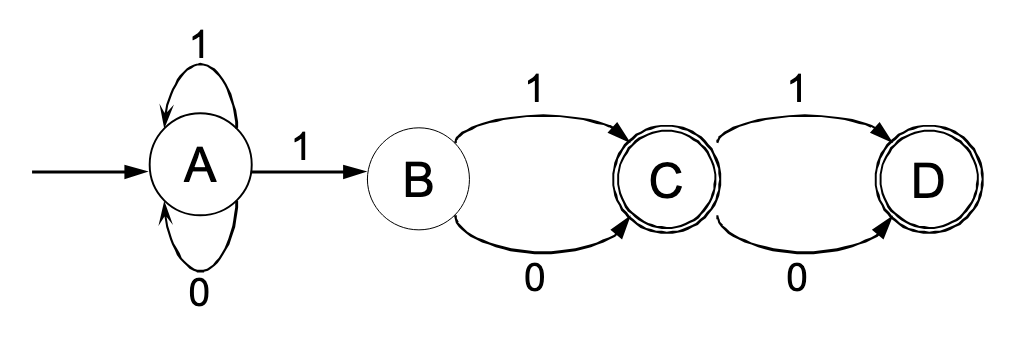
VNEA:

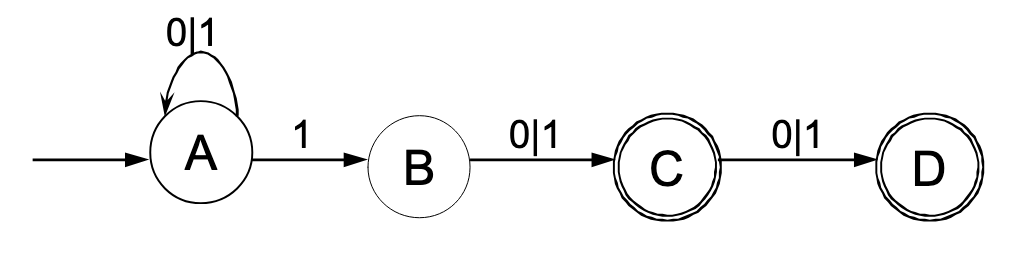
1. Elimination für Endzustand C & D:

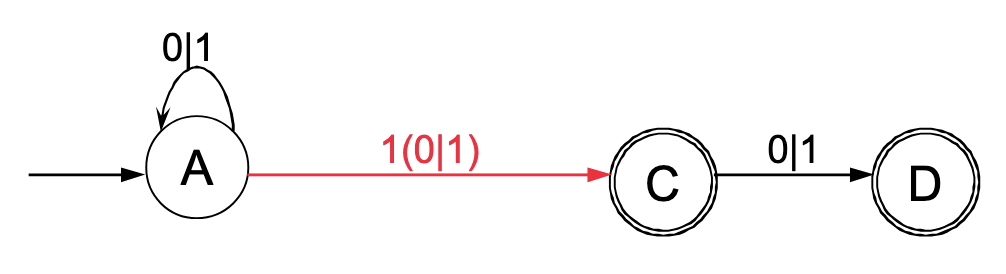
2. Elimination für Endzustand C:

2. Elimination für Endzustand D:

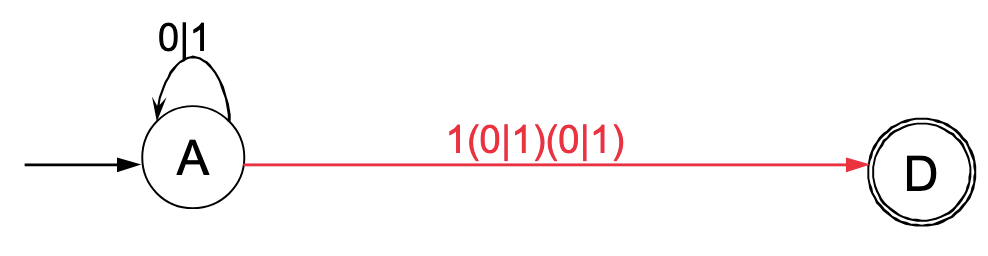
Kombination:

• Endzustand C: (0|1)*1(0|1)
• Endzustand D: (0|1)*1(0|1)(0|1)
• Kombiniert: (0|1)*1(0|1) | (0|1)*1(0|1)(0|1)
• Optimiert: (0|1)*1(0|1)(ε|(0|1))

Kellerautomaten

Ein EA kann sich nur bestimmt viele Zustände “merken”. Eine Sprache, bei der man Zählen muss und bei der die Obergrenze nicht bekannt ist, lässt sich also nicht darstellen. Ein Kellerautomat ist ein Automat, der Zugriff auf einen “Kellerspeicher” (Stack) hat. Er kann also Dinge speichern. Der Stack ist zudem theoretisch unendlich, was bedeutet, dass er z.B. zum Zählen verwendet werden kann.

Ein Kellerautomat ist definiert als:

$$\text{KA}=(S,\Sigma ,\Gamma ,\delta ,s_0,\perp ,F)$$

Symbole:

• $S$: Endliche Menge von Zuständen
• $\Sigma$: Endliches Eingabealphabet
• $\Gamma$: Endliches Kelleralphabet
• $\delta$: Übergangsrelation $\delta :(S\times (\Sigma \cup \{ϵ\})\times \Gamma )\to \underline{P}(S\times {\Gamma }^{\ast })$
• $s_0$: Anfangszustand $s_0\in S$
• $\perp$: Keller-Bottomsymbol $\perp \in \Gamma$
• $F$: Endzustandsmenge $F\subseteq S$

⇒ Ein Standard-Kellerautomat ist nichtdeterministisch! Nur wenn die Übergangsrelation eindeutig ist spricht man von einem deterministischen Kellerautomaten (DKA/DPDA). Im Gegensatz zu normalen endlichen Automaten sind ein KA und DKA nicht äquivalent, d.h. der DKA erkennt nur eine echte Teilmenge der vom KA erkannten Sprachen.

Kellerautomaten können auch ohne Endzustandsmenge ($\text{KA}=(S,\Sigma ,\Gamma ,\delta ,s_0,\perp )$) definiert werden. Dann akzeptiert der KA eine Eingabe, falls nach der Abarbeitung der Eingabe der Keller leer ist. Wenn der KA nichtdeterministisch ist, sind die beiden Varianten (mit und ohne Endzustandsmenge) äquivalent. Zu jedem KA existiert außerdem ein äquivalenter KA ohne ε-Übergänge.

Zustandsüberführung

Die Zustandsüberführung bei Kellerautomaten funktionieren so:

$$\delta (s,a,A)=\{(s^{\prime },B_1...B_k),(s^{\prime \prime },C_1...C_m),(s^{\prime \prime \prime },N_1...N_n)\}$$

Bedeutet:

• Wenn sich der Kellerautomat gerade im Zustand $s$ befindet,
  • gerade das Zeichen $a$ liest und
  • $A$ das oberste Kellersymbol ist,
• dann kann der Kellerautomat in den Zustand $s^{\prime }$ wechseln
  • und dabei $A$ durch das Wort $B_1...B_k$ ersetzen

Dies lässt sich am einfachsten Schreiben als:

$$(s,a,A,s^{\prime },B_1...B_k)$$

Bedeutung der Symbole:

• $s$: Aktueller Zustand
• $a$: Gelesenes Zeichen
• $A$: Oberstes Kellersymbol
• $s^{\prime }$: Neuer Zustand
• $B_1...B_k$: Neues Wort, wodurch $A$ überschrieben wird

Konfiguration

Jeder Kellerautomat benötigt außerdem eine Konfiguration $K$, die den aktuellen Zustand $s$, das noch zu verarbeitende Suffix $w$ des Eingabewortes und den aktuellen Kellerinhalt $\alpha$ beinhaltet:

$$K=(s,w,\alpha )\in S\times {\Sigma }^{\ast }\times {\Gamma }^{\ast }$$

Konfigurationsübergänge

Ein Konfigurationsübergang ist festgelegt durch die Relation $(S\times {\Sigma }^{\ast }\times {\Gamma }^{\ast })\times (S\times {\Sigma }^{\ast }\times {\Gamma }^{\ast })$. Wenn also eine Zustandsüberführung $(s,a,A,s^{\prime },\beta )$ Teil der Übergangsrelation $\delta$ ist, ist automatisch $(s,av,A\alpha )\to (s^{\prime },v,\beta \alpha )$ ein valider Übergang, durch den das oberste Kellersymbol ($A$) gelöscht und durch ein neues Wort $\beta$ ersetzt wird.

Akzeptierte Sprachen

Eine von einem Kellerautomat $K=(S,\Sigma ,\Gamma ,\delta ,s_0,\perp ,F)$ akzeptierte Sprache ist definiert als:

$$L(K)=\{w\in {\Sigma }^{\ast }\text{ | }(s_0,w,\perp ){\to }^{\ast }(s_f,ϵ,\gamma ),s_f\in F,\gamma \in {\Gamma }^{\ast }\}$$

Erklärung der Symbole:

• $w\in {\Sigma }^{\ast }$: Ein Eingabewort $w$ muss in der Summe aller Wörter enthalten sein.
• $(s_0,w,\perp ){\to }^{\ast }(s_f,ϵ,\gamma )$: Es muss möglich sein, vom Startzustand $s_0$ mit dem Eingabewort $w$ bei einem leeren Keller ($\perp$) auf einen Endzustand $s_f$ zu gelangen, bei dem das Eingabewort gänzlich gelesen wurde ($ϵ$) und etwas ($\gamma$) im Keller steht.
• $s_f\in F$: Der Endzustand muss in der Zustandsmenge des Automaten enthalten sein
• $\gamma \in {\Gamma }^{\ast }$: Das Wort im Keller muss im Kelleralphabet enthalten sein

Falls der Automat auch bei leerem Keller akzeptieren soll, kann die Sprache definiert werden als:

$$L(K)=\{w\in {\Sigma }^{\ast }\text{ | }(s_0,w,\perp ){\to }^{\ast }(s_f,ϵ,\gamma ),s\in S\}$$

⇒ Der Zustand, der nach Einlesen des Wortes erreicht ist, muss Teil der definierten Zustände des Kellerautomaten sein.

Übergangsrelationen

Eine einfachere Schreibweise für die Übergangsrelationen $\delta$ des Kellerautomaten lautet:

$$\delta =\{(\text{Aktueller Zustand},\text{Symbol},\text{Kellersymbol 0},\text{Neuer Zustand},\text{Neuer Input})\}$$

• Aktueller Zustand: Der aktuelle Zustand, in dem sich der Kellerautomat befindet
• Symbol: Das eingelesene Symbol
• Kellersymbol 0: Das oberste Kellersymbol
• Neuer Zustand: Der Zustand, in den der Automat wechseln soll
• Input für Keller: Was anstelle von Kellersymbol 0 geschrieben werden soll (Kellersymbol 0 wird beim Lesen entfernt)

⇒ Wenn sich der Kellerautomat im aktuellen Zustand befindet, Symbol eingelesen wird und das oberste Kellersymbol gleich Kellersymbol 0 ist, soll der Automat in den neuen Zustand übergehen und den neuen Input in den Stack schreiben.

Kontextfreie Sprachen

Mit einer kontextfreien Sprache lassen sich die regulären Sprachen (aber auch weitere Sprachen) ausdrücken. Eine Kontextfreie Sprache kann z.B. durch eine kontextfreie Grammatik beschrieben werden.

Grammatik

Eine Grammatik ist ein Tupel $G=(\Sigma ,N,P,S)$:

• $\Sigma$: Terminal-Alphabet
• $N$: Nonterminal-Alphabet (Variablen)
• $P$: Produktionenmenge (Regelmenge)
• $S$: Startsymbol

Großbuchstaben sind Variablen, S ist (meist) das Startsymbol. Kleinbuchstaben sind Terminale. Die Großbuchstaben $X$, $Y$ und $Z$ sind Symbole, die als Terminale und Variablen genutzt werden können.

Die Kleinbuchstaben $u$ bis $z$ sind Zeichenketten aus anderen Terminalen und die griechischen Kleinbuchstaben $\alpha$, $\beta$, $\gamma$, … sind Zeichenketten aus Variablen und Terminalen (beide sind Variablen für größere Zeichenketten).

Für die Darstellung einer Grammatik genügt die Angabe der Produktionen, da die Konventionen aus den Variablen, Terminalen und dem Startsymbol hergeleitet werden können.

Außerdem können Produktionen zusammengefasst werden:

$$A\to {\alpha }_1,A\to {\alpha }_2,A\to {\alpha }_2$$

kann mit dem ODER-Operator geschrieben werden als

$$A\to {\alpha }_1\text{ | }{\alpha }_2\text{ | }{\alpha }_3$$

Eine Grammatik heißt kontextfrei, falls für ihre Regelmenge gilt:

$$P\subseteq N\times (\Sigma \cup N{)}^{\ast }\text{ mit }|P|<\infty$$

d.h. falls jede Regel die Form $P:A\to \alpha$ hat.

Kontextfreie Sprache

Eine Sprache $L$ heißt kontextfrei, wenn es eine kontextfreie Krammatik $G$ mit $L(G)=L$ gibt (Solche Sprachen werden auch Typ-2-Sprachen genannt).

Ableitung

Eine Ableitung beschreibt, wie man vom Startsymbol zu einem Wort der Sprache $L$ kommt. Ein Ableitungsschritt ($\to$) ist hierbei die Ersetzung eines Nichtterminals durch eines oder mehrere (Nicht-) Terminale. Die Ableitung endet, wenn keine Nichtterminale mehr auftreten.

Transitive Hülle

Die transitive Hülle ${\to }^{\ast }$ des Ableitungsschritts bezeichnet die gesamte Ableitung bis zu einem Wort:

$$E{\to }^{\ast }id+(id\ast id)$$

Es gilt also:

$$L(G)=\{w\in \Sigma \text{ | }S{\to }^{\ast }w\}$$

⇒ Für jedes Wort der Grammatik muss man aus einem Zustand irgendwie das Wort erreichen können.

Links-/Rechtsableitung

Eine Links- bzw. Rechtsableitung beschreibt eine Ableitung, bei der immer nur das am weitesten links/rechts stehende Nichtterminal ersetzt wird.

Linksableitung:

$$S\to aAS\to aSbAS\to aaabAS\to aabbaS\to aabbaa$$

Rechtsableitung:

$$S\to aAS\to aAa\to aSbAa\to aSbbaa\to aabbaa$$

Ableitungsbäume

Zu einer kontextfreien Grammatik kann ein Baum $t$ erstellt werden, der die Ableitung symbolisiert. Damit ein Baum als Ableitungsbaum bezeichnet werden darf, müssen folgende Bedingungen erfüllt sein:

• Die Wurzel muss mit $S$ markiert sein
• Jeder Knoten ist mit $X\in N\cup \Sigma \cup \{ϵ\}$ (einem (Nicht-) Terminal) markiert
• Jeder innere Knoten ist mit einem $A\in N$ (einem Nichtterminal) markiert
• Wenn ein innerer Knoten mit $A\in N$ (einem Nichtterminal) markiert ist und seine Nachfolger von links nach rechts mit $X_1,...X_n\in N\cup \Sigma \cup \{ϵ\}$ (einem Terminal), dann muss $A\to X_1...X_n\in P$ sein.
• Wenn ein Knoten $k$ mit $ϵ$ markiert ist, ist $k$ ein Blatt und der einzige Sohn seines Vaters

Beispiel:

Ableitungsbaum für die Linksableitung

$$S\to aAS\to aSbAS\to aaabAS\to aabbaS\to aabbaa$$

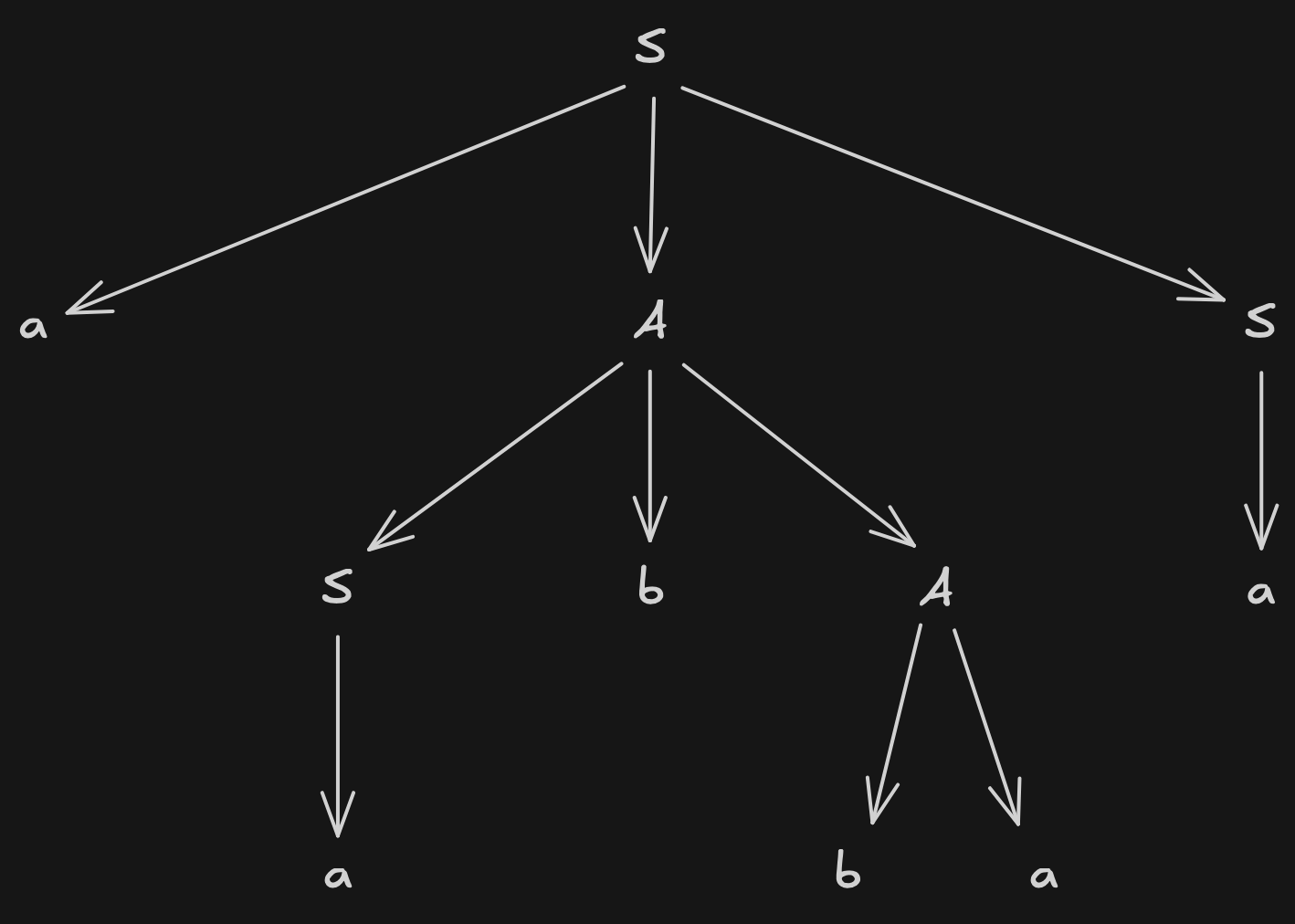
Ein Ableitungsbaum ist eine natürliche Beschreibung für die Ableitung einer bestimmten Satzform der Grammatik G, die man erhält, wenn man die Markierungen aller Blätter von links nach rechts liest. Diese Zeichenkette wird auch Front des Ableitungsbaumes genannt:

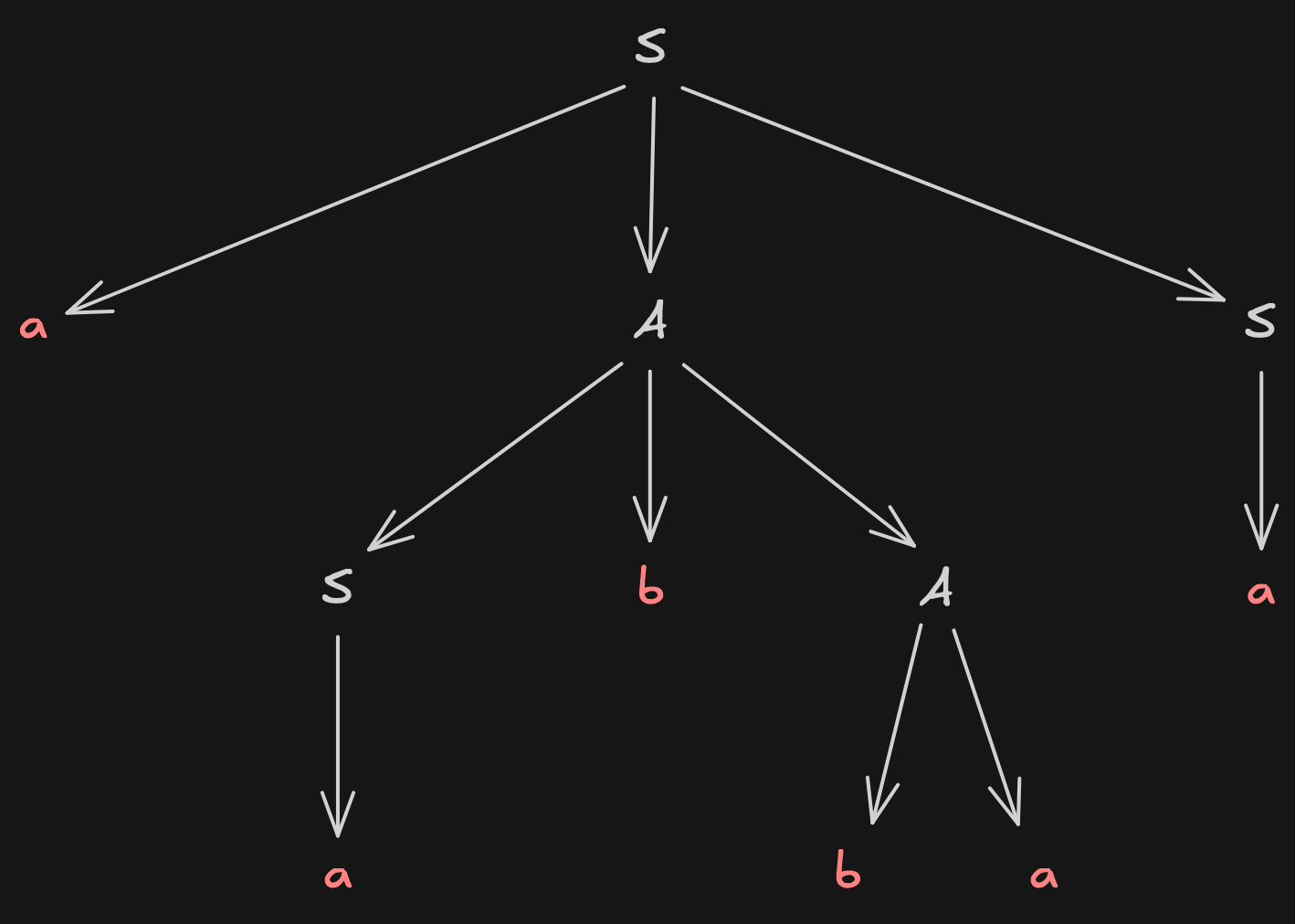
Achtung!

Zu einer Satzform können mehrere Ableitungsbäume existieren.

Mehrdeutigkeit

Eine kontextfreie Grammatik heißt mehrdeutig, falls es für mindestens ein Wort $w\in L(G)$ zwei (oder mehr) verschiedene Ableitungsbäume gibt, oder falls mindestens ein Wort $w\in L(G)$ mehr als eine Links-/Rechtsableitung hat. Eine kontextfreie Sprache, die für jede kontextfreie Grammatik.

Vereinfachungen

Ziel bei der Vereinfachung ist, das Format der Produktionen einzuschränken, ohne deren Fähigkeit zur Erzeugung von Sprachen zu beschneiden. Eine kontextfreie Grammatik lässt sich durch folgende Maßnahmen vereinfachen:

• Eliminierung von ε-Regeln: Es gibt keine Produktionen der Form $A\to ϵ$ wenn $ϵ\notin L$
• Eliminieren nutzloser Symbole: Jede Variable und jedes Terminal von $G$ erscheint in der Ableitung mindestens eines Wortes aus $L$
• Eliminieren von Kettenregeln: Es gibt keine Produktionen der Form $A\to B$, wenn $A$ und $B$ Variablen sind

Eliminieren von ε-Regeln

1. Bestimme alle Nichtterminale, die in ein ε umgewandelt werden können: $N^{\prime }=\{A\in N\text{ | }A\to ϵ\}$
2. Bestimme alle Nichtterminale, aus denen das leere Wort ableitbar ist: $N^{\prime \prime }=\{A\in N\text{ | }A{\to }^{\ast }ϵ\}$
3. Für jede Regel, deren Rechte Seite ein Nichtterminal aus $N^{\prime \prime }$ enthält, fügen wir eine Regel ohne dieses Nichtterminal hinzu.
4. Eliminiere alle ε-Regeln (entferne das ε aus allen Umformungen und entferne die Umformung selbst, falls das ε nicht verodert ist)

Beispiel:

$S\to AB$ $A\to ϵ\text{ | }B$ $B\to b$

Hier führt $A$ zu einem leeren Wort, also “markieren” wir es im 1. Schritt. Da sich $A$ aus $S$ ableiten lässt, markieren wir auch dies. In Schritt 3 wird $S$ umgeformt, da wir das $A$ in der Ableitung dort markiert haben:

$S\to AB\text{ | }B$ $A\to ϵ\text{ | }B$ $B\to b$

Im letzten Schritt entfernen wir das ε aus der Ableitung von $A$:

$S\to AB\text{ | }B$ $A\to B$ $B\to b$

Eliminieren nutzloser Symbole

Beim Eliminieren von nutzlosen Symbolen wird darauf geachtet, welche Symbole nützlich für die Grammatik $G$ sind. Ein Symbol $X$ heißt nützlich, wenn mit seiner Hilfe mindestens ein Terminalwort erzeugt werden kann, also wenn gilt:

$$S{\to }^{\ast }\alpha X\beta {\to }^{\ast }w$$

mit $\alpha ,\beta \in (N\cup \Sigma {)}^{\ast }$ und $w\in {\Sigma }^{\ast }$.

Beim Eliminieren von nützlichen Symbolen wird also darauf geachtet, dass zwei Aspekte der Nützlichkeit für jedes Symbol gegeben sind:

1. Aus $X$ muss eine Terminalzeichenkette ableitbar sein (Lemma 1)
2. $X$ muss Teil einer Zeichenkette sein, die aus $S$ ableitbar ist (Lemma 2)

Lemma 1 beschäftigt sich mit der Erreichbarkeit von Symbolen. Ein Symbol muss erreichbar sein, also vom Startsymbol aus in einer Folge von Produktionen irgendwann erzeugt werden. Bei Lemma 1 werden alle Symbole, die niemals vom Startsymbol aus erreicht werden können, eliminiert. Der Algorithmus hierzu sieht so aus:

1. Merke dir alle Nichtterminale, die per Ableitung in ein Terminal verwandelt werden können ($N_2=\{A\text{ | }A\to w\text{ fu¨r ein }w\in {\Sigma }^{\ast }\}$ ⇒ A muss ein Nichtterminal produzieren, was in der Menge aller Wörter steht)
2. Prüfe, welche Ableitungen zu den gemerkten Nichtterminalen führen, und markiere diese, bis alle Ableitungen durchlaufen sind. Sobald alle anderen Ableitungen angeschaut und markiert sind, entferne alle nicht markierten Ableitungen.

Lemma 2 hingegen eliminiert nicht erzeugende Symbole. Ein Symbol ist erzeugend, wenn es ein Wort bestehend aus nur Terminalsymbolen ableiten kann. Alle Symbole, die kein terminales Wort erzeugen können, sind ebenfalls nutzlos.

1. Starte bei $S$ und durchlaufe alle möglichen Ableitungen, um zu sehen, welche Nichtterminale erreicht werden können. Entferne alle Ableitungen, die nicht erreicht werden können.

Eliminieren von Kettenregeln

Kettenregeln sind Regeln mit folgender Form:

$$A\to B\text{ mit }A,B\in N$$

Sie tragen zur Erzeugung eines Wortes nichts bei. Kettenregeln können mit 3 Schritten eliminiert werden:

1. Entfernen von Zyklen: Gibt es Nichtterminale, die einen Zyklus erzeugen (z.B. $A_1\to A_2\to A_3\to A_1$), fügen wir ein neues Nichtterminal $A$ hinzu und ersetzen alle $A_i$ durch $A$.
2. Umnummerierung: $N$ hat nun $n$ Elemente. Wir bezeichen diese mit $A_1,...,A_n$, so dass gilt: Wenn $A_i\to A_j$, dann ist $i<j$
3. Ersetzen von Kettenregeln: Wenn noch Regeln wie $A_i\to A_j$ dann kann jede Regel $A_j\to w$ ersetzt werden durch $A_i\to w$

Im folgenden Beispiel gibt es keine Zyklen, daher müssen diese nicht entfernt werden (Lemma 1 nicht zutrefflich). Auch Lemma 2 ist nicht zutrefflich, da alle Nichtterminale von $S$ aus erreicht werden können.

$S\to A\text{ | }B$ $A\to B$ $B\to b$

Allerdings existieren Kettenregeln, die entfernt werden können: $S\to A\to B$ ist equivalent zu $S\to B$. Außerdem kann $S\to B\to b$ vereinfacht werden zu $S\to b$.

$$S\to b$$

Damit ist die Vereinfachung abgeschlossen.

Chomsky-Normalform (CNF)

Eine kontextfreie Grammatik ist in CNF, wenn alle ihre Produktionen eine der folgenden Formen haben:

1. $A\to BC$
2. $A\to a$
3. $A\to ϵ$ (nur vorhanden, wenn $G$ das leere Wort erzeugt)

(mit $A,B,C,S\in N$ und $a\in \Sigma$)

⇒ Zu jeder kontextfreien Sprache $L$ lässt sich eine Grammatik $G$ in CNF angeben, so dass $L(G)=L$ ist.

Zum Erzeugen der CNF einer Grammatik muss die Grammatik maximal vereinfacht vorliegen. Man beachte die Produktionen $A\to X_1{X}_2...X_m$:

• Wenn $X_i=a\in \Sigma$ vorhanden ist: Ersetze $X_i$ durch $C_a$, füge neue Produktion $C_a\to a$ hinzu, ersetze alle anderen $a$ durch $C_a$.
• Wenn kein $X_i=a\in \Sigma$ vorhanden ist: Betrachte die Produktion $A\to B_1{B}_2...B_m$ und ersetze dies durch die Produktionen $A\to B_1{D}_1,D_1\to B_2{D}_2,...,D_{m-2}\to B_{m-1}{B}_m$.

Wortproblem & CYK-Algorithmus

Wenn eine kontextfreie Grammatik $G$ in der CNF sowie ein Wort $w$ gegeben sind, stellt sich die Frage, ob das Wort $w$ Teil der Sprache $L(G)$ ist ($w\in L(G)$). Dies kann mit dem Cocke-Younger-Kasami-Algorithmus (CYK) beantwortet werden.

Die Idee lautet wiefolgt: Für jedes Teilwort $w$ der Sprache $L$ wird die Menge der Nichtterminale berechnet, die benötigt werden, um das Wort zu erzeugen. Man dringt hierbei von kleineren zu immer größeren Teilwörtern vor. Am Einfachsten ist dies Tabellarisch zu erreichen.

Beispiel

• Gesuchtes Wort $w=bbabaa$
• Produktionen:
  • $S\to AB\text{ | }BC$
  • $A\to BA\text{ | }a$
  • $B\to CC\text{ | }b$
  • $C\to AB\text{ | }a$

Es wird eine Tabelle mit $n$ Zeilen und $n$ Spalten aufgestellt, wobei $n=|w|$:

$V_{i,j}$	1	2	3	4	5	6
1
2	------
3	------	------
4	------	------	------
5	------	------	------	------
6	------	------	------	------	------

Entlang der Hauptdiagonalen werden dann die Terminale von $w$ eingetragen:

$V_{i,j}$	1	2	3	4	5	6
1	b
2	------	b
3	------	------	a
4	------	------	------	b
5	------	------	------	------	a
6	------	------	------	------	------	a

Dann werden die Terminale durch die möglichen Nichtterminale, durch die sie direkt erzeugt werden können ersetzt:

$V_{i,j}$	1	2	3	4	5	6
1	B
2	------	B
3	------	------	A, C
4	------	------	------	B
5	------	------	------	------	A, C
6	------	------	------	------	------	A, C

Hier beginnt der Algorithmus. Zuerst schauen wir uns $V_{1,2}$ an. Da es keine Produktion gibt, die $BB$ erzeugt, tragen wir ”{}” ein:

$V_{i,j}$	1	2	3	4	5	6
1	B	{}
2	------	B
3	------	------	A, C
4	------	------	------	B
5	------	------	------	------	A, C
6	------	------	------	------	------	A, C

Bei $V_{2,3}$ hingegen gibt es Produktionen, die entweder $BA$ oder $BC$ erzeugen, weshalb wir die Terminale für die Produktionen ($S,A$) dort eintragen:

$V_{i,j}$	1	2	3	4	5	6
1	B	{}
2	------	B	S, A
3	------	------	A, C
4	------	------	------	B
5	------	------	------	------	A, C
6	------	------	------	------	------	A, C

Weiter geht es danach mit $V_{1,3}$, $V_{3,4}$, $V_{2,4}$, $V_{1,4}$, $V_{4,5}$, $V_{3,5}$ usw. Nachdem die ganze Tabelle ausgefüllt wurde, sieht sie wie folgt aus:

$V_{i,j}$	1	2	3	4	5	6
1	B	{}	A	S, C	B	A, S
2	------	B	S, A	S, C	B	A, S
3	------	------	A, C	S, C	B	S, A
4	------	------	------	B	S, A	{}
5	------	------	------	------	A, C	B
6	------	------	------	------	------	A, C

Nachdem die Tabelle gefüllt ist, muss in der oberen rechten Ecke das Startsymbol $S$ zu finden sein. Falls es vorhanden ist, ist das Wort $w$ in der Sprache $L(G)$ enthalten.

Reguläre Grammatiken

Bisher wurden reguläre Sprachen und kontextfreie Sprachen behandelt. Zur Wiederholung, eine reguläre Sprache ist beschrieben durch einen regulären Ausdruck oder ein Syntaxdiagramm und wird akzeptiert durch endliche Automaten. Eine kontextfreie Sprache hingegen wird durch eine kontextfreie Grammatik beschrieben und von (nichtdeterministischen) Kellerautomaten akzeptiert.

Reguläre Sprachen können aber auch durch eine eigene Grammatik beschrieben werden.

⇒ Eine Sprache ist genau dann regulär, wenn sie durch eine reguläre Grammatik erzeugt wird.

Links-/Rechtslinearität

Eine kontextfreie Grammatik, deren Produktionen alle die Form

$$A\to Bw\text{ | }w$$

besitzen, heißt linkslinear. Genauso heißt eine kontextfreie Grammatik, deren Produktionen alle die Form

$$A\to wB\text{ | }w$$

besitzen rechtslinear.

⇒ ==Eine Grammatik heißt regulär, wenn sie rechtslinear oder linkslinear ist.==

Grenzen kontextfreier Sprachen

(TODO)

Linear bandbeschränkte Automaten (LBA)

Reguläre Sprachen haben ebenfalls Grenzen. Eine Sprache bei der man “zählen” muss und bei der die Obergrenze nicht bekannt ist, lässt sich nicht als reguläre Ausdrücke darstellen. Die Sprache

$$L=\{a^k{b}^k{c}^k\text{ | }k>0\}$$

beispielsweise kann nicht durch eine kontextfreie Grammatik erzeugt werden. Das Hauptproblem liegt darin, dass bei den Kellerautomaten und bei kontextfreien Sprachen das Lesen aus dem Stack das gelesene Element zerstört. Es ist also nicht möglich, eine Information vom Stack zu lesen und für später aufzuheben.

Die Lösung hierfür sind linear bandbeschränkte Automaten (LBAs). Anstelle des Stacks verwenden sie ein “Band” als Speichermedium, ähnlich einem Magnetband. Das Band wird von einem endlichen Automaten mit “Schreib-Lese-Kopf” gelesen und beschrieben. Der Kopf steht immer über einem Feld des Bandes. In einem Schritt:

• liest der Kopf das Symbol auf dem Band,
• schreibt, falls nötig, ein neues Symbol,
• ändert seinen Zustand und
• führt eine Bewegung nach rechts oder links aus

Zu Beginn der Verarbeitung befindet sich die Eingabe auf dem Band selbst. Wie der Name des Automaten vermuten lässt, ist er nach rechts und links beschränkt, seine Länge ist also endlich. Dies wird über Start- und Ende-Zeichen realisiert, die nicht überschrieben werden können. Die formale Definition des Automaten lautet:

$$\text{LBA}=(S,\Sigma ,\Gamma ,\delta ,s_0,\text{␣},\Lleftarrow ,\Rrightarrow ,F)$$

Wobei:

• $S$ die endliche Menge an Zuständen symbolisiert
• $\Sigma$ für das endliche Eingabealphabet steht ($\Sigma \subseteq \Gamma ,\text{␣}\notin \Sigma$)
• $\Gamma$ das Symbol für das endliche Bandalphabet ist
• $\delta$ die Übergangsrelation $\delta :(S\times {\Gamma }^{\ast })\to (S\times \Gamma \times \{L,R\})$
• $s_0$ der Anfangszustand ist ($s_0\in S$)
• $\text{␣}$ das Leerzeichen darstellt ($\text{␣}\in \Gamma$)
• $\Rrightarrow$ für die linke Endmarkierung steht
• $\Lleftarrow$ für die rechte Endmarkierung steht
• $F$ die Endzustandsmenge verkörpert ($F\subseteq$ S)

Weitere Symbole, die nicht direkt in der Definition enthalten sind:

• ${\Gamma }^{\ast }$ ist das erweiterte Bandalphabet inklusive der Start- und Endsymbole (${\Gamma }^{\ast }=\Gamma \cup \{\Rrightarrow ,\Lleftarrow \}$)

Die Übergangsrelationen bei diesen Automaten werden wie folgt geschrieben:

${\delta }_{ex}=(\text{Zustand},\text{Gelesenes Symbol},\text{Neuer Zustand},\text{Geschriebenes Symbol},\text{Bewegung})$

Eine einzelne Übergangsrelation (hier ${\delta }_{ex}$ genannt) aus einem Zustand $s_0$ bei einem gelesenen Zeichen $\Rrightarrow$ zu Zustand $s_1$, bei der nichts (das leere Wort) geschrieben wird, und sich der Schreib-Lese-Kopf nach rechts bewegt, sieht also so aus:

$${\delta }_{ex}=(s_0,\Rrightarrow ,s_1,ϵ,R)$$

Kontextsensitive Sprachen

Der LBA ist equivalent zu einer kontextsensitiven Grammatik. Eine Grammatik gilt als kontextsensitiv, wenn ihre Produktionen die Form

$$P:{\alpha }_{1}A{\alpha }_2\to {\alpha }_1\beta {\alpha }_2$$

haben: das Nichtterminal $A$ kann nur im Kontext ${\alpha }_1...{\alpha }_2$ ersetzt werden! ${\alpha }_1$ und ${\alpha }_2$ dürfen auch leer sein, eine kontextsensitive Grammatik kann also auch kontextfreie Produktionen zulassen.

Eine kontextsensitive Grammatik ist monoton, wenn ihre Produktionen die Form

$$P:\alpha \to \beta$$

mit $|\alpha |\le |\beta |$ haben.

Sprache

Eine Sprache $L$ heißt kontextsensitiv, wenn es eine kontextsensitive Grammatik $G$ mit $L(G)=L$ gibt. Kontextsensitive Sprachen (Grammatiken) werden auch Typ-1-Sprachen (-Grammatiken) genannt.

Rekursiv aufzählbare Sprachen

Eine Grammatik $G=(\Sigma ,N,P,S)$ ist ein Semi-Thue-System, wenn ihre Produktionen die Form

$$P:\alpha \to \beta \text{ mit }\alpha ,\beta \in {\Sigma }^{\ast }$$

haben. Die Besonderheit bei einem Semi-Thue-System ist, dass eigentlich keine Unterscheidung zwischen Terminalen und Nichtterminalen existiert. Es werden zwar Nichtterminale verwendet, allerdings sind die Produktionen in keiner Weise eingeschränkt. Rekursiv aufzählbare Sprachen werden von Turing-Maschinen akzeptiert.

Die Turing-Maschine

Die Turing-Maschine hat, genau wie der LBA:

• Ein “Band” als Speichermedium
• Einen Schreib-Lese-Kopf

Der Kopf steht auch hier immer über einem Feld des Bandes und liest in einem Schritt das Symbol, schreibt optionaler ein neues Symbol, ändert seinen Zustand und führt eine Bewegung aus. Auch bei der Turing-Maschine befindet sich die Eingabe zu Beginn bereits auf dem Band. Es gibt jedoch folgende Unterschiede zum LBA:

• Das Band ist nach rechts und links unbeschränkt (es ist unendlich lang)
• Alle Zellen außer der Eingabe sind mit “Blank” gefüllt

Eine Turing-Maschine ist definiert als:

$$\text{TM}=(S,\Sigma ,\Gamma ,\delta ,s_0,\text{␣},F)$$

Wobei:

• $S$ die endliche Menge an Zuständen symbolisiert
• $\Sigma$ für das endliche Eingabealphabet steht ($\Sigma \subseteq \Gamma ,\text{␣}\notin \Sigma$)
• $\Gamma$ das Symbol für das endliche Bandalphabet ist
• $\delta$ die Übergangsrelation $\delta :(S\times {\Gamma }^{\ast })\to (S\times \Gamma \times \{L,R\})$
• $s_0$ der Anfangszustand ist ($s_0\in S$)
• $\text{␣}$ das Leerzeichen darstellt ($\text{␣}\in \Gamma$)
• $F$ die Endzustandsmenge verkörpert ($F\subseteq$ S)

Eine Übergangsrelation (hier ${\delta }_{ex}$) bei einer Turing-Maschine sieht so aus:

$${\delta }_{ex}=(\text{Zustand},\text{Gelesenes Symbol},\text{Neuer Zustand},\text{Geschriebenes Symbol},\text{Bewegungsrichtung})$$

Bei einem Zustand $s_0$, gelesenem Symbol $a$ und einem darauffolgenden Zustandsübergang in $s_1$, wobei ein $X$ geschrieben wird und der Kopf sich nach links bewegt, sieht die Übergangsrelation so aus:

$${\delta }_{ex}=(s_0,a,s_1,X,R)$$

Darstellung

Eine Turing-Maschine kann auch visuell dargestellt werden:

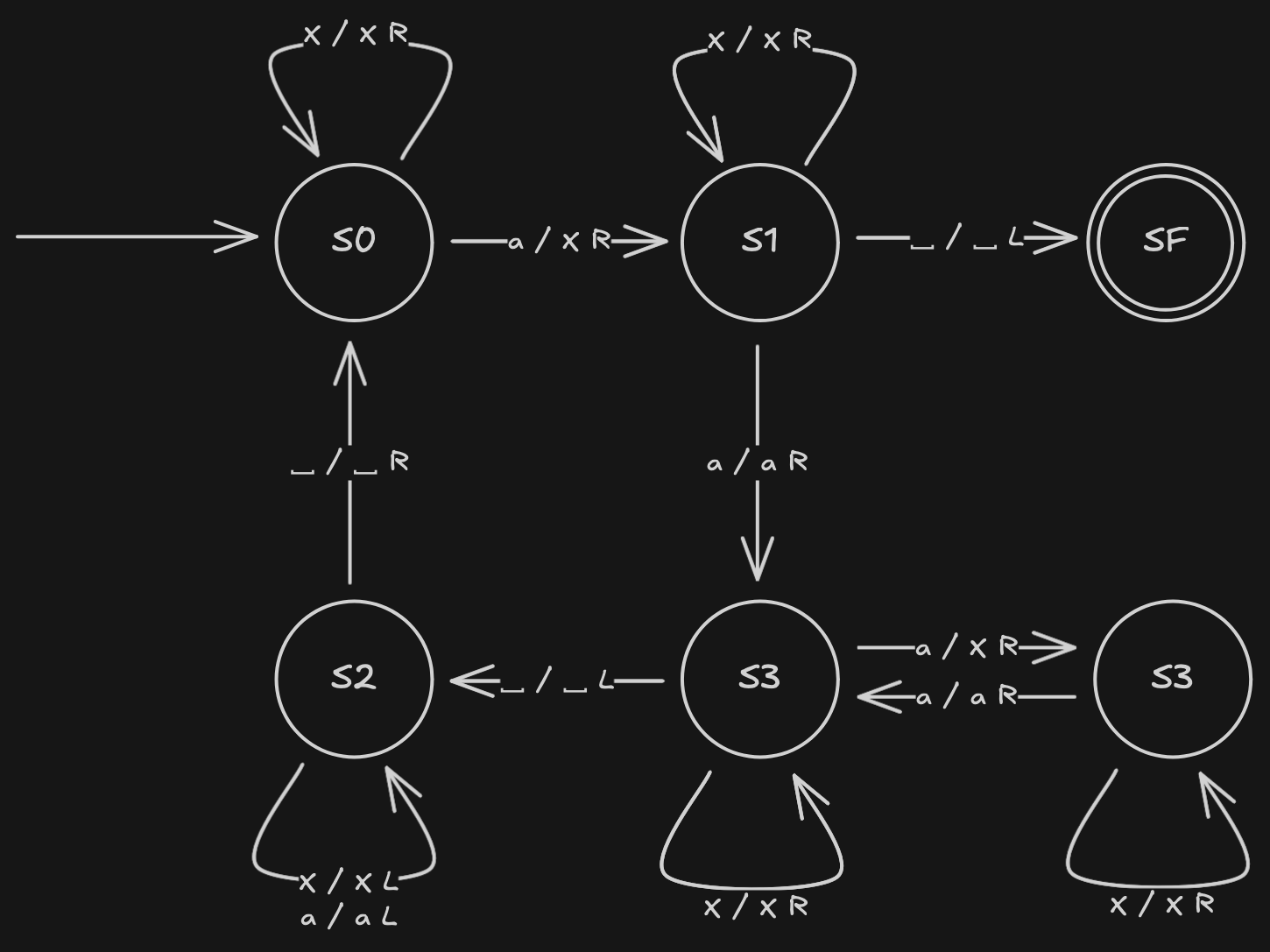
Die Übergange auf den Pfeilen werden gelesen als: $\text{(Gelesen) / (Geschrieben) (Bewegung)}$.

Erweiterungen von Turing-Maschinen

Das “Programmieren” von Turing-Maschinen ist schwierig, aber es gibt Möglichkeiten, um die TM effizienter zu programmieren. Keine dieser Möglichkeiten erweitert die Fähigkeiten der Turing-Maschine, alle akzeptieren dieselbe Menge von Sprachen wie das Basismodell. Mögliche Erweiterungen für die TM sind:

• Das Speichern einer endlichen Datenmenge im Zustand
• Ein Band aus mehreren Spuren
• Unabhängig bewegbare Schreib-/Leseköpfe auf mehreren Bändern

Nichtdeterministische Turing-Maschinen

Turing-Maschinen können Nichtdeterministisch sein. Wie bei einem NEA können für jeden Zustand und für jedes Bandsymbol mehrere Übergange existieren. Die NTM wählt immer den geeigneten Übergang aus (Hellsehen / Backtracking.)

Berechenbarkeit mit Turing-Maschinen

Mithilfe einer Turing-Maschine kann man Probleme auf ihre Berechenbarkeit untersuchen. Dazu benötigt man eine TM, die in einen akzeptierenden Zustand übergeht und anhält, sobald sie ein Wort als zu einer Sprache zugehörig erkennt. Wenn ein Wort nicht zu einer Sprache gehört, also abgelehnt werden soll, geht sie in einen nicht akzeptierenden Zustand über und hält ebenfalls an. Das Anhalten signalisiert das Ende der Berechnung.

Die von einer TM akzeptieren Sprachen heißen rekursiv aufzählbar. Bei einem Wort, das zur Sprache gehört, hält die TM nach endlich vielen Schritten an. Allerdings gibt es keine Festlegung, was die TM macht, wenn ein Wort nicht zur Sprache gehört. Es gibt also eventuell Wörter, die zur nicht zur Sprache gehören, für die die TM aber auch nie anhält.

Rekursive Sprachen

Eine Sprache $L=L(M)$ heißt rekursiv, wenn für die Turing-Maschine $M$ gilt:

• Wenn das Wort zur Sprache gehört, akzeptiert $M$ nach endlich vielen Schritten und hält an.
• Wenn das Wort nicht zur Sprache gehört, hält $M$ nach endlich vielen Schritten ebenfalls an, geht aber in keinen akzeptierenden Zustand über.

Die rekursiven Sprachen sind eine echte Teilmenge der rekursiv aufzählbaren Sprachen. Eine TM, die eine rekursive Sprache akzeptiert, entspricht der Definition eines Algorithmus, also einer Berechnung, die nach endlich vielen Schritten anhält.

⇒ Rekursive Sprachen $\ne$ Rekursiv aufzählbare Sprachen!

Berechenbarkeit

Bei der Berechenbarkeit geht es um die Frage von Alan Turing, was Computer theoretisch berechnen können, und was nicht. Dabei geht es immer um die Ein- und Ausgabemöglichkeiten der Computer. Eingaben können beispielsweise von Tastatur und Maus kommen, und Ausgaben können über Bildschirme und Lautsprecher gemacht werden. Die Kernkompetenz eines Programms liegt also darin, Eingaben in Ausgaben abzubilden.

Formal kann man diese Abbildung definieren als:

$$f:{\Sigma }^{\ast }\to {\Gamma }^{\ast }$$

(${\Sigma }^{\ast }$ ist das Eingabealphabet, ${\Gamma }^{\ast }$ das Ausgabealphabet.)

Falls die Funktion $f$ nicht sämtliche mögliche Eingaben ${\Sigma }^{\ast }$ akzeptiert, sondern nur eine Teilmenge $\text{def}(f)\subseteq {\Sigma }^{\ast }$ davon, spricht man von einer partiellen Funktion:

$$f:\text{def}(f)\to {\Gamma }^{\ast }$$

Wenn eine Eingabe $x$ nicht abbildbar ist, schreibt man:

$$f(x)=\perp$$

($\perp =\text{Undefiniert}$)

Eine partielle Funktion $f$ nennt man berechenbar, falls es einen Algorithmus gibt, der diese Funktion berechnet. Wie die Alphabete $\Sigma$ und $\Gamma$ dabei tatsächlich aussehen ist eigentlich egal. Man kann sie immer durch ein Binärwort kodieren. Die Art der Kodierung ist nicht vorgeschrieben und kann für jedes Ein- und Ausgabealphabet anders definiert sein.

Algorithmus

Es gibt nicht wirklich einen einzigen Algorithmus zum Lösen solcher Probleme. Vielmehr gilt: Wenn es möglich ist, eine Funktion in irgendeiner Programmiersprache zu programmieren, ist die Funktion sicher berechenbar.

Satz von Cantor

Der Satz von Cantor besagt, dass für jede Menge $M$ die Menge ihrer Teilmengen (Die Potenzmenge $P(M)$) strikt größer ist als $M$ selbst ($|P(M)|>|M|$)

Nicht berechenbare Funktionen

Da Programme einen endlichen Quelltext besitzen, muss es (sehr viele) Funktionen geben, die nicht durch ein Programm berechnet werden können. Die Berechenbarkeit ist davon abhängig, was ein Algorithmus kann / darf.

Church’sche These

“Jede Präzisierung des Begriffes Algorithmus führt auf die gleiche Menge berechenbarer Funktionen.”

⇒ Man kann prinzipiell auf jedem Rechner jeden anderen Rechner simulieren. Die Hardware ist nicht entscheidend für die Berechenbarkeit einer Funktion. Die Programmiersprache ist ebenfalls nicht entscheidend.

Halteproblem der TM

Es ist nicht möglich, einen Algorithmus zu definieren, der für jede Turing-Maschine und für jede Eingabe berechnet, ob die Turing-Maschine mit dieser Eingabe anhält.

Fehlend: Stoff von Folien 452 bis 461!

Turing-Maschinen in Binärdarstellung

Eine Turing-Maschine $M=(S,\Sigma ,\Gamma ,\delta ,s_0,\text{␣},F)$ kann in eine Binärzeichenkette umgewandelt werden, indem allen Symbolen, Zuständen und Richtungen eindeutige Binärcodes zugewiesen werden.

Jede Übergangsfunktion $\delta :(q_i,X_j)=(q_k,X_l,D_m)$ wird als Binärfolge kodiert:

$$C_n=0^{i}10^{j}10^{k}10^{l}10^m$$

⇒ Niemals zwei Einsen hintereinander!

Dann werden alle Übergangscodes durch zwei Einsen zusammengefügt:

$$A_M=C_{1}11C_2\mathrm{11...}{C}_{n-1}11C_n$$

$A_M$ kodiert so die Turing-Maschine $M$.

Compilerbau

TODO: Noch nicht in der Vorlesung gehört.

---

Klausurthemen

• Sprache/Automat in Chomsky-Hierarchie einordnen
• Umwandlung NEA/DEA
• RE → NEA → DEA → RE
• Übergangsdiagramm ⇐> Syntaxdiagramm (Darstellung)
• Sprache (alle Wörter) aus RE/RG erzeugen
• lexikographische Ordnung
• Spache in Automat (dreierrest Binärzahl)
• Ableitungsbäume
• Pumping Lemma, Halteproblem TM → Multiple Choice
• Compilerbau (nur Grob) → LL(1)-Grammatiken, FIRST/FOLLOW
• Algorithmen:
  • Potenzmengenkonstruktion
  • Baukastenmethode (RE → NEA → DEA → RE)
  • Zustandselimination
  • Minimierung EA
  • Minimierung von kfG, Erzeugung CNF aus kfG
  • CYK-Alg. (Wortproblem)

---

TODO

• Pumping Lemma
• Berechenbarkeit
  • Halteproblem
• Compilerbau
  • Einführung
    • Definition
    • Compiler-Phasen
      • Frontend
      • Backend
    • Vergleich zu Interpreter
    • Programmtext
  • Lexikalische Analyse
    • Probleme & heutiger Ansatz
  • Syntaxanalyse
    • Parser
    • Grammatik
    • Ableitung
    • Eindeutige Grammatiken
    • Termbäume
  • Recursive Descent Parset
  • LL(1)-Grammatiken
  • Top-Down Parsing
  • Shift-Reduce-Parser
  • LR(1)-Grammatiken
  • Parsergeneratoren
  • Bison
  • Fehlererkennung
  • Symboltabellen
  • Codeoptimierung